A Framework for Powerful Math Instruction - Part 2
By Sandye Kabalen (someone who had to re-learn math to really teach it)
![]() In
Part 1, I shared how discovering the Effective Mathematics Teaching Practices (EMTPs)
gave me the language and direction I had been missing.
In
Part 1, I shared how discovering the Effective Mathematics Teaching Practices (EMTPs)
gave me the language and direction I had been missing.
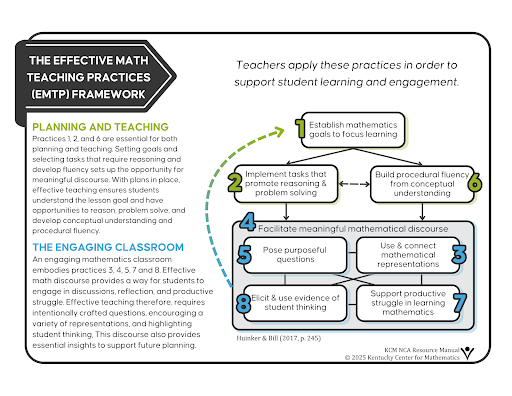
1. Establish mathematics goals to focus learning.
2. Implement tasks that promote reasoning and problem solving.
3. Use and connect mathematical representations.
4. Facilitate meaningful mathematical discourse.
5. Pose purposeful questions.
6. Build procedural fluency from conceptual understanding.
7. Support productive struggle in learning mathematics.
8. Elicit and use evidence of student thinking. (Principles to Actions, p. 10)
They helped me shift from teaching procedures to supporting real understanding. But what truly changed my classroom was realizing that these practices don't work in isolation. It wasn't about picking one or two to focus on. It was about how they fit together. In this post, I'll share what it looked like when I started using the practices as a connected framework and how that shift helped me create a classroom where students were thinking deeply and engaging with the math in meaningful ways.
(If you haven't read Part 1 yet, you can click here for a link to read that post.)
How the Practices Work Together:
One of the biggest lessons I learned early on was that no single strategy could “fix” everything. What made a difference was when I started thinking about my instruction as a whole, how each part of the lesson connected to the next, and how every decision I made was either supporting student thinking or shutting it down.
The eight teaching practices don't live in isolation. They're interconnected. For example:
- When I introduced open-ended tasks that encourage reasoning, I had to facilitate meaningful discourse to help students make sense of those tasks.
- When I supported students through productive struggle, I realized how important it was to have clear goals and a strong grasp of the math myself.
- And when I truly started listening to student thinking, it reshaped the questions I asked and the feedback I gave.
Thinking of the practices as a connected framework, rather than a checklist, was a major shift for me. It helped me stop trying to control every step and start focusing on what students were doing and understanding.
NCTM introduced this framework in a series of books in 2017, Taking Action: Implementing Effective Mathematics Teaching Practices. These books were especially helpful because they show what the practices look like in real classrooms with real students.
How the Framework Is Organized:
The EMTP Framework mirrors the natural flow of teaching, starting with planning, moving into instruction, which then informs planning. Planning and teaching are a cycle, and everything should keep coming back to the goals to keep learning focused and meaningful.
Click here for a link to a printable version of the NCTM Effective Math Teaching Practices.
Planning and Teaching:
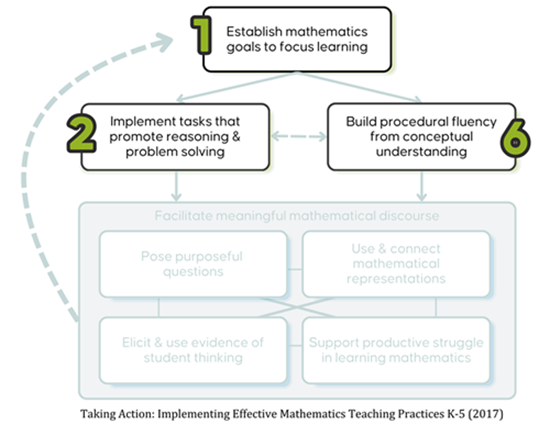 Math Teaching Practice #1 (Establishing Clear Goals) sits at the top of the EMTP Framework, emphasizing that everything we do in the
classroom should begin with clear, purposeful goals grounded in academic standards. I used to think I was doing this, but looking back,
my goals were more about getting through content than ensuring understanding. Once I started writing goals that were student-centered
and rooted in the big ideas of the standard, my lessons became more focused and meaningful.
Math Teaching Practice #1 (Establishing Clear Goals) sits at the top of the EMTP Framework, emphasizing that everything we do in the
classroom should begin with clear, purposeful goals grounded in academic standards. I used to think I was doing this, but looking back,
my goals were more about getting through content than ensuring understanding. Once I started writing goals that were student-centered
and rooted in the big ideas of the standard, my lessons became more focused and meaningful.
Next came choosing tasks that would actually support these goals (Practice #2), and making sure they allowed for reasoning, not
just rote steps. I also had to think about how to build fluency (Practice #6). Instead of beginning with notes and teaching the
algorithm first, I needed to begin with models and conversations, building the why before the how. Because of this, students were
more confident, less dependent on me, and more willing to take risks.
In short, Practices 1, 2, and 6 are the heart of planning. When I focused first on setting clear goals, choosing rich tasks, and connecting them to conceptual understanding, my lessons were intentional and my students were more engaged right from the start.
The Engaging Classroom:
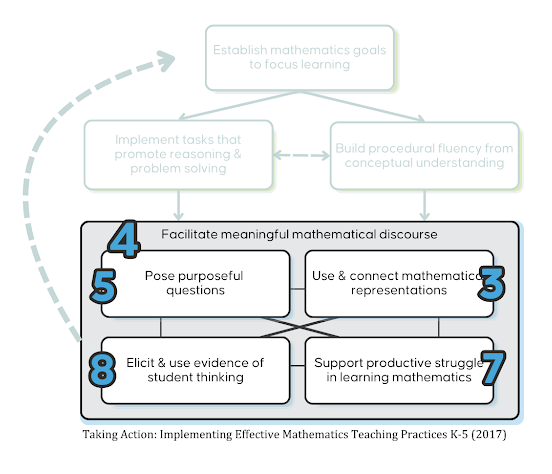 This is the part of the framework that helped me bring my classroom to life. Facilitating math discourse (Practice #4) became the heart
of my instruction. I used to think “discussion” meant calling on students who raised their hands. Instead, it means providing ALL students
with opportunities to explain, critique, and reflect on the mathematics and each other's ideas.
This is the part of the framework that helped me bring my classroom to life. Facilitating math discourse (Practice #4) became the heart
of my instruction. I used to think “discussion” meant calling on students who raised their hands. Instead, it means providing ALL students
with opportunities to explain, critique, and reflect on the mathematics and each other's ideas.
To do this, I began planning my questions (Practice #5) and using those questions to make use of student thinking (Practice #8).
I started paying attention to how students were reasoning, not just whether they were right.
Encouraging students to use their own strategies and representations (Practice #3) gave them multiple ways to express their understanding.
I stopped thinking of drawings and manipulatives as something only struggling students needed and began using them as tools for ALL students
to build and connect ideas.
Supporting productive struggle (Practice #7) was the toughest one for me. I had to resist jumping in too soon and realize that struggle is when the real learning happens.
Looking back, it was in this part of the framework, during the actual facilitation of student learning, where I grew the most as a teacher. It pushed me to listen more, trust my students' thinking, and let go of some control. In doing that, I created a classroom where EVERY student had a voice, made sense of the math in their own way, and truly began to understand.
Conclusion:
Looking back, I'm grateful for the discomfort I felt when I didn't know how to model fraction division because it forced me to become the kind of teacher I wish I had been sooner. The Effective Mathematics Teaching Practices gave me the tools and the language for a kind of teaching that was more rewarding. Because when we teach math for understanding, we don't just teach better - we reach more students. And that changes everything.
Resources:
Principles to Actions — Executive Summary (PDF)



![]() Effective Mathematics Teaching Practices Collection
Effective Mathematics Teaching Practices Collection
Related Posts
 A Framework for Powerful Math Instruction - Part 1
A Framework for Powerful Math Instruction - Part 1 Standards for Mathematical Practice (SMPs)
Standards for Mathematical Practice (SMPs) The Effective Mathematics Teaching Practices
The Effective Mathematics Teaching Practices EMTP 1: Establish Mathematics Goals to Focus Learning
EMTP 1: Establish Mathematics Goals to Focus Learning EMTP 2: Implement Tasks that Promote Reasoning and Problem Solving
EMTP 2: Implement Tasks that Promote Reasoning and Problem Solving EMTP 3: Use and Connect Mathematical Representations
EMTP 3: Use and Connect Mathematical Representations EMTP 4: Facilitate Meaningful Mathematical Discourse
EMTP 4: Facilitate Meaningful Mathematical Discourse EMTP 5: Pose Purposeful Questions
EMTP 5: Pose Purposeful Questions EMTP 6: Build Procedural Fluency from Conceptual Understanding
EMTP 6: Build Procedural Fluency from Conceptual Understanding EMTP 7: Support Productive Struggle in Learning Mathematics
EMTP 7: Support Productive Struggle in Learning Mathematics EMTP 8: Elicit and Use Evidence of Student Thinking
EMTP 8: Elicit and Use Evidence of Student Thinking