Problemas con Triángulos

Objetivos

Al concluir esta lección, deberás ser capaz de:

Seleccionar el método adecuado para resolver un problema que involucre triángulos.
Obtener los lados o ángulos de un triángulo.
Resolver problemas verbales con triángulos.

Introducción

Hasta el momento, hemos estudiado tres métodos diferentes que nos ayudarán a resolver problemas que involucran triángulos:

Usando las razones trigonométricas que aprendimos en la lección Trigonometría de Triángulos Rectángulos.
La Ley de Senos.
La Ley de Cosenos.

En esta lección aprenderás a seleccionar el método adecuado para resolver problemas con triángulos. Resolveremos varios problemas verbales y no verbales que involucran en su solución encontrar las medidas de los lados o ángulos de un triángulo.

Selección del Método

Como vimos en las lecciones de Ley de Senos y Ley de Cosenos, cuando resolvemos problemas que involucran triángulos podemos encontrar los siguientes casos:

Si el triángulo es rectángulo, la mejor forma de resolverlo es usando las razones trigonométricas que aprendimos en la lección Trigonometría de Triángulos Rectángulos.

Si el triángulo es oblicuo, entonces se pueden presentar los siguientes casos:

Caso	Método
1. Se conoce un lado y dos ángulos
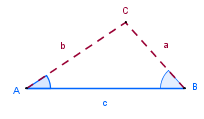
ALA	Ley de Senos
LAA	Ley de Senos
2. Se conocen dos lados y el ángulo opuesto a uno de estos lados
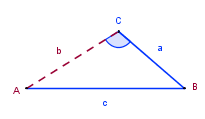
LLA	Ley de Senos
3. Se conocen dos lados y el ángulo entre ellos
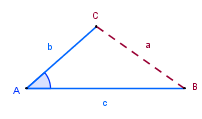
LAL	Ley de Cosenos
4. Se conocen los tres lados
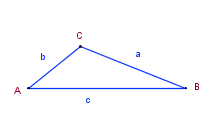
LLL	Ley de Cosenos

Es importante notar que para definir en forma única un triángulo debemos conocer al menos tres elementos del conjunto de sus lados y ángulos, entre los cuales debe estar incluido por lo menos uno de los lados.

Resolver un triángulo significa encontrar todos los valores de sus lados y ángulos.

El siguiente árbol de decisiones nos ayudará a determinar el método adecuado para resolver un problema:

flow_diag

Hallar los Lados o Angulos de un Triángulo

Ejemplo 1:

En el triángulo de la figura, hallar la longitud del lado rotulado con x

Rect

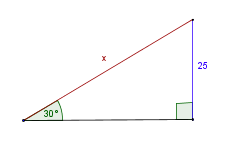
Solución:

El triángulo de la figura es rectángulo. Por lo tanto, utilizamos las razones trigonométricas.

La función trigonométrica que relaciona un ángulo con el lado opuesto y la hipotenusa es la función seno.

Obteniendo el valor de x usando la razón trigonométrica correspondiente a la función seno:

$sen (30°) = \frac{25}{x}$

donde:

$x = \frac{25}{sen (30°)}$

$x = 50$

Ejemplo 2:

En el triángulo de la figura, hallar la longitud del lado rotulado con x

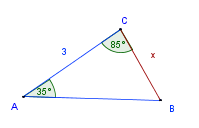
ex1lal

Solución:

El triángulo de la figura es oblicuo y se conoce un lado y dos ángulos (Caso 1 ALA). Por lo tanto, utilizamos la Ley de Senos.

Obteniendo la medida del ángulo B.

B = 180° −35° − 85° = 60°

Obteniendo el valor de x mediante la Ley De Senos:

$\frac{x}{sen (35°)} = \frac{3}{sen (60°)}$

donde:

$x = \frac{3 sen (35°)}{sen (60°)}$

$x \approx 1.99$

Ejemplo 3:

Encontrar la longitud del lado b y las medidas de los ángulos A y C en el siguiente triángulo:

ex1lal

Solución:

Como conocemos dos lados adyacentes y el ángulo entre ellos, podemos aplicar la Ley de Cosenos, así:

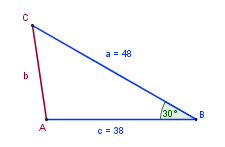1. Hallando b:

$b^{2} = a^{2} + c^{2} - 2 a c \cos (B)$

$b^{2} = 48^{2} + 38^{2} - 2 (48) (36) \cos (30°)$

$b^{2} = 1444 + 2304 - (2) (1824) (\frac{\sqrt{3}}{2})$

$b^{2} = 136 - 60$

$b^{2} \approx 588.74$

$b \approx 24.3$

2. Ahora que conocemos el valor de b, podemos hallar A utilizando la Ley de Senos:

$\frac{sen (A)}{48} = \frac{sen (30°)}{24.3}$

donde:

$sen (A) = \frac{48 sen (30°)}{24.3}$

$sen (A) \approx 0.99$

Como vimos en la lección de la Ley de Senos, este es el caso ambiguo:

Tenemos las siguientes posibilidades para A:

$A \approx 81°$ o $A \approx 99°$

En la figura de arriba, trazamos los valores iniciales del problema a escala. Observemos que el ángulo A es obtuso (mayor de 90°) Por lo tanto , $A \approx 99°$

3. Hallando C

C = 180° −30° − 99° = 51°

Problemas Verbales

Ejemplo 1:

Una persona de 6 pies de estatura, está parada a 20 pies de un poste de alumbrado público y proyecta una sombra de 10 pies de longitud. ¿Cuál es la altura de el poste?

Solución:

Ilustremos la situación que se describe en el problema: un persona que proyecta una sombra producida por un poste de alumbrado público.

Sobre la gráfica anterior, ubiquemos los datos del problema:

En la figura, observemos que se forman dos triángulos rectángulos: ABE y CDE.

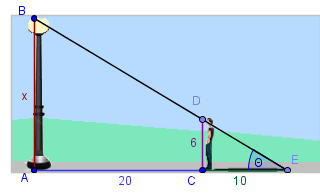
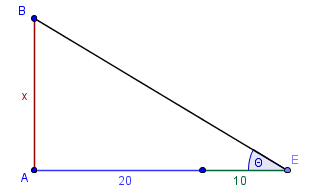
ex1lal

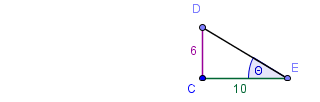
Para el ángulo θ en la la figura de la izquierda, se cumple:

Considerando el triángulo ABE

$\tan (θ) = \frac{x}{20 + 10}$

Considerando el triángulo CDE

$\tan (θ) = \frac{6}{10}$

Como ambas expresiones son iguales, entonces:

\frac{x}{20 + 10} = \frac{6}{10}

donde:

x = \frac{6 (30)}{10}

x = 18

Respuesta: La altura del poste de alumbrado es 18 pies.

Ejemplo 2:

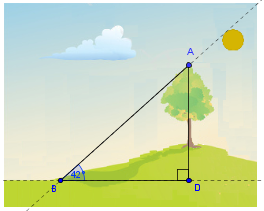
Un árbol de 10 metros proyecta una sombra de 17 metros por una pendiente cuando el ángulo de elevación del sol es de 42°. Buscar el ángulo de elevación del terreno.

Solución:

Ilustremos la situación que se describe en el problema: un árbol que proyecta una sombra en un terreno con cierta elevación.

Sobre la gráfica anterior, ubiquemos los datos del problema:

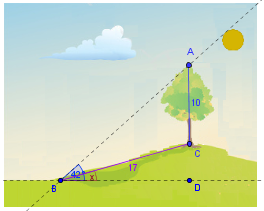
En la figura, observemos el triángulo rectángulo ABD.

ex1lal

En la la figura de la izquierda, podemos obtener el ángulo A, así.

A = 90° − 42° = 48°

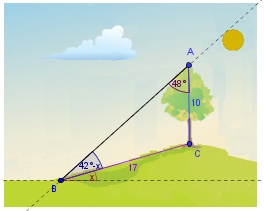
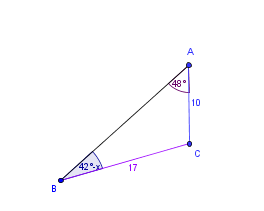
Ya que conocemos A, ahora podemos utilizar el triángulo ABC, para obtener x. Nota que el ángulo B es 42° - x.

ex1lal

Conocemos dos lados y el ángulo opuesto a uno de ellos. Siguiendo las pautas de la primera sección, debemos usar la Ley de Senos para obtener el ángulo B = 42°-x.

$\frac{sen (42° - x)}{10} = \frac{sen (48°)}{17}$

donde:

$sen (42° - x) = \frac{10 sen (48°)}{17}$

$42° - x = {sen}^{-1} (\frac{10 sen (48°)}{17})$

$42° - x \approx 26°$

$x \approx 42° - 26°$

$x$ ≈ 16°

Como este es el caso ambiguo, hay que verificar la otra posibilidad, es decir que:

$42° - x \approx 180° - 26° = 154°$

Este valor para el ángulo B es imposible, pues si sumamos con el ángulo A da un valor mayor a 180°

Respuesta: El ángulo de elevación del terreno es aproximadamente 16°

Ejemplo 3:

Para aproximar la longitud de un pantano, un topógrafo camina 400 metros del punto B al punto C, luego gira 60° y camina 500 metros al punto A. Aproximar la longitud AB del pantano.

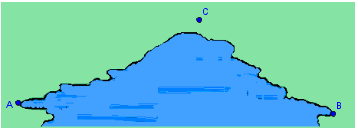
ex1lal

Solución:

Imaginemos primero la situación que se describe en el problema: un árbol que proyecta una sombra en un terreno con cierta elevación.

Sobre la gráfica anterior, ubiquemos los datos del problema:

Vemos que en la figura, se forma un triángulo oblicuo.

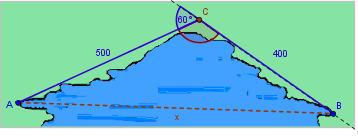
ex1lal

En la la figura de la izquierda, podemos obtener el ángulo C del triángulo, así.

C = 180° − 60° = 120°

Ahora podemos utilizar el triángulo ABC, para obtener x.

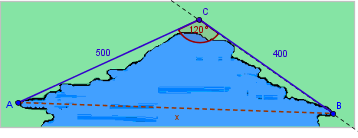
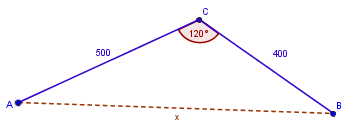
ex1lal

Conocemos dos lados y el ángulo entre ellos. Siguiendo las pautas de la primera sección, debemos usar la Ley de Cosenos para obtener el lado x.

$x^{2} = 500^{2} + 400^{2} - 2 (500) (400) \cos (120°)$

$x^{2} = 250000 + 160000 - (2) (200000) (- \frac{1}{2})$

$x^{2} = 410000 + 200000$

$x^{2} = 610000$

$x \approx 781$

Respuesta: La longitud del punto AB del pantano es aproximadamente 781 metros.

Resumen

Ahora que has completado esta lección, eres capaz de:

Seleccionar el método adecuado para resolver un problema que involucre triángulos.
Obtener los lados o ángulos de un triángulo.
Resolver problemas verbales con triángulos.