Solución de Sistemas de Ecuaciones Lineales

Objetivos

Al concluir esta lección, deberás ser capaz de:

Resolver sistemas de ecuaciones lineales por el método de sustitución.
Resolver sistemas de ecuaciones lineales por el método de eliminación.

Introducción

En esta lección vamos a estudiar los métodos para la solución de sistemas de ecuaciones:

Método de Sustitución.
Método de Eliminación.

Método de Sustitución

Para resolver un sistema de ecuaciones usando el método de sustitución, seguiremos los siguientes pasos:

Resolver para una variable. Seleccionar una de las ecuaciones y obtener una variable en términos de la otra variable.
Sustituir con la expresión. Utilizar la expresión obtenida en el paso 1 para sustiuir la variable correspondiente en la ecuación que no se utilizó en el paso 1.
Sustituir con el valor obtenido. Sustituir en la expresión obtenida en el paso 1, el valor de la variable encontrado en el paso anterior.
Verificar. Es una buena práctica verificar los resultados para ssegurarnos que no cometimos errores.

Ejemplo 1:

Utilizar el método de sustitución para encontrar la solución del siguiente sistema de ecuaciones:

${\begin{matrix} x - y = 2 \\ 2 x + 3 y = 9 \end{matrix}$

Solución:

$\begin{matrix} x - y = 2 \\ x = 2 + y \end{matrix}$

Paso 1: Resolver para una variable.

Resolviendo para x en la primera ecuación:

$\begin{matrix} x - y = 2 \\ x = 2 + y \end{matrix}$

Paso 2:Sustituir con la expresión obtenida.

Sustituimos la expresión que obtuvimos en el paso anterior x = 2 + y en la segunda ecuación y resolvemos para y.

$\begin{matrix} 2 x + 3 y = 9 \\ 2 (2 + y) + 3 y = 9 \\ 4 + 2 y + 3 y = 9 \\ 4 + 5 y = 9 \\ 4 + 5 y - 4 = 9 - 4 \\ 5 y = 5 \\ \frac{5 y}{5} = \frac{5}{5} \\ y = 1 \end{matrix}$

Paso 3:Sustituir con el valor obtenido.

Sustituir en la expresión obtenida en el paso 1, el valor de y = 1, obtenido en el paso anterior.

$\begin{matrix} x = 2 + y \\ x = 2 + 1 \\ x = 3 \end{matrix}$

Solución: La solución del sistema de ecuaciones es x =3, y =1. También se puede escribir la solución como un par ordenado (3,1)

Verificación

La solución obtenida (3,1) debe satisfacer ambas ecuaciones.

$\begin{matrix} x - y = 2 \\ 3 - 1 = 2 \\ 2 = 2 \end{matrix}$

$\begin{matrix} 2 x + 3 y = 9 \\ 2 (3) + 3 (1) = 9 \\ 6 + 3 = 9 \\ 9 = 9 \end{matrix}$

Gráfica

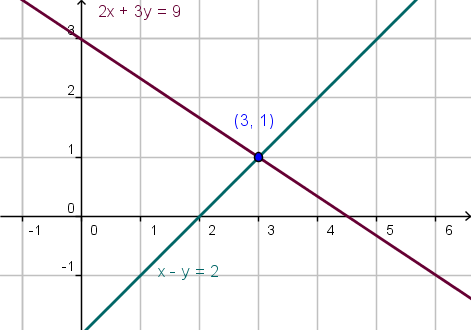
Gráficamente podemos ver que la solución del sistema es la intersección de las rectas representadas por las ecuaciones.

sus x1

Paso 1: Resolver para una variable.

Resolviendo para x en la segunda ecuación:

$\begin{matrix} x - 2 y = - 8 \\ x = 2 y - 8 \end{matrix}$

Paso 2:Sustituir con la expresión..

Sustituimos la expresión que obtuvimos en el paso anterior x = 2y-8 en la primera ecuación y resolvemos para y.

$\begin{matrix} 2 x + y = -1 \\ 2 (2 y - 8) + y = -1 \\ 4 y - 16 + y = - 1 \\ 5 y - 16 = - 1 \\ 5 y - 16 + 16 = - 1 + 16 \\ 5 y = 15 \\ \frac{5 y}{5} = \frac{15}{5} \\ y = 3 \end{matrix}$

Paso 3:Sustituir con el valor obtenido.

Sustituir en la expresión obtenida en el paso 1, el valor de y = 3, obtenido en el paso anterior.

$\begin{matrix} x = 2 y - 8 \\ x = 2 (3) - 8 \\ x = 6 - 8 \\ x = - 2 \end{matrix}$

Solución: La solución del sistema de ecuaciones es x =-2, y =3. También se puede escribir la solución como un par ordenado (-2,3)

Verificación

La solución obtenida (-2,3) debe satisfacer ambas ecuaciones.

$\begin{matrix} 2 x + y = -1 \\ 2 (- 2) + 3 = -1 \\ -4 + 3 = -1 \\ -1 = -1 \end{matrix}$

$\begin{matrix} x - 2 y = - 8 \\ - 2 - 2 (3) = - 8 \\ -2 - 6 = -8 \\ -8 = -8 \end{matrix}$

Gráfica

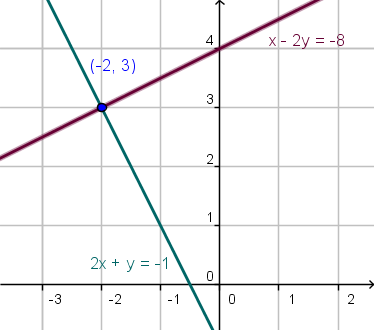
Gráficamente podemos ver que la solución del sistema es la intersección de las rectas representadas por las ecuaciones.

sus x1

Paso 1: Ajustar los coeficientes.

Multiplicamos ambos lados de la primera ecuación por -2, con el fin de que los coeficientes de x difieran solo en signo.

${\begin{matrix} (- 2) \end{matrix} \begin{matrix} (x + 2 y) & = & (- 2) 5 \\ 2 x + 3 y & = & 8 \end{matrix}$

Obtenemos este sistema de ecuaciones equivalente:

${\begin{matrix} - 2 x - 4 y & = & - 10 \\ 2 x + 3 y & = & 8 \end{matrix}$

Paso 2:Sumar los lados correspondientes de las ecuaciones. Resolver para la variable que no fue eliminada.

Recordemos que si tenemos dos ecuaciones,

a = b

c = d

entonces se cumple que a + c = b + d.

Vamos a aplicar este hecho al sistema obtenido en el paso anterior.

Sumando los lados correspondientes de ambas ecuaciones y resolviendo para y

$\begin{matrix} \underline{{\begin{matrix} - 2 x & - 4 y & = & - 10 \\ 2 x & + 3 y & = & 8 \end{matrix}} \\ \begin{matrix} - 2 x - 4 y + 2 x + 3 y & = & - 10 + 8 \\ - y & = & - 2 \\ y & = & 2 \end{matrix} \end{matrix}$

Paso 3:Sustituir con el valor obtenido.

Sustituir el valor de y=2 que encontramos en el paso anterior en cualquiera de las ecuaciones originales. Utilizaremos la primera ecuación, pues se ve más sencilla, y resolveremos para la variable x.

$\begin{matrix} x + 2 y = 5 \\ x + 2 (2) = 5 \\ x + 4 = 5 \\ x + 4 - 4 = 5 - 4 \\ x = 1 \end{matrix}$

Solución: La solución del sistema de ecuaciones es x =1, y =2. También se puede escribir la solución como un par ordenado (1,2)

Verificación

La solución obtenida (1,2) debe satisfacer ambas ecuaciones.

$\begin{matrix} x + 2 y = 5 \\ 1 + 2 (2) = 5 \\ 1 + 4 = 5 \\ 5 = 5 \end{matrix}$

$\begin{matrix} 2 x + 3 y = 8 \\ 2 (1) + 3 (2) = 8 \\ 2 + 6 = 8 \\ 8 = 8 \end{matrix}$

Gráfica

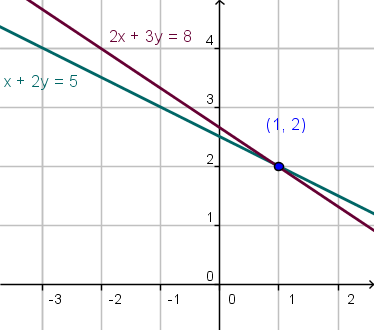
Gráficamente podemos ver que la solución del sistema es la intersección de las rectas representadas por las ecuaciones.

sus x1

Paso 1: Ajustar los coeficientes.

Multiplicamos ambos lados de la segunda ecuación por 3, con el fin de que los coeficientes de y difieran solo en signo.

${\begin{matrix} (3) \end{matrix} \begin{matrix} 4 x - 3 y & = & 11 \\ (2 x + y) & = & (3) 3 \end{matrix}$

Obtenemos este sistema de ecuaciones equivalente:

${\begin{matrix} 4 x - 3 y & = & 11 \\ 6 x + 3 y & = & 9 \end{matrix}$

Paso 2:Sumar los lados correspondientes de las ecuaciones. Resolver para la variable que no fue eliminada.

Recordemos que si tenemos dos ecuaciones,

a = b

c = d

entonces se cumple que a + c = b + d.

Vamos a aplicar este hecho al sistema obtenido en el paso anterior.

Sumando los lados correspondientes de ambas ecuaciones y resolviendo para y

$\begin{matrix} \underline{{\begin{matrix} 4 x - 3 y & = & 11 \\ 6 x + 3 y & = & 9 \end{matrix}} \\ \begin{matrix} 4 x - 3 y + 6 x + 3 y & = & 11 + 9 \\ 10 x & = & 20 \\ x & = & 2 \end{matrix} \end{matrix}$

Paso 3:Sustituir con el valor obtenido.

Sustituir el valor de x=2 que encontramos en el paso anterior en cualquiera de las ecuaciones originales. Utilizaremos la segunda ecuación, pues se ve más sencilla, y resolveremos para la variable y.

$\begin{matrix} 2 x + y = 5 \\ 2 (2) + y = 3 \\ 4 + y = 3 \\ 4 + y - 4 = 3 - 4 \\ y = -1 \end{matrix}$

Solución: La solución del sistema de ecuaciones es x =2, y =-1. También se puede escribir la solución como un par ordenado (2,-1)

Verificación

La solución obtenida (2,-1) debe satisfacer ambas ecuaciones.

$\begin{matrix} 4 x - 3 y = 11 \\ 4 (2) - 3 (-1) = 11 \\ 8 - (-3) = 11 \\ 8 + 3 = 11 \\ 11 = 11 \end{matrix}$

$\begin{matrix} 2 x + y = 3 \\ 2 (2) + (-1) = 3 \\ 4 - 1 = 3 \\ 3 = 3 \end{matrix}$

Gráfica

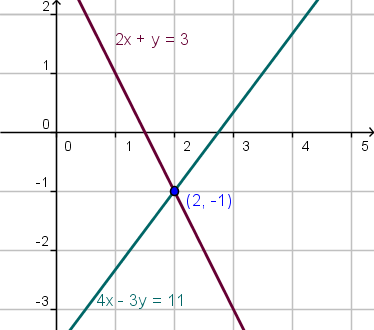
Gráficamente podemos ver que la solución del sistema es la intersección de las rectas representadas por las ecuaciones.

sus x1


Haz Click en los botones para ver los pasos de la Solución

Ejemplo 2:

Utilizar el método de sustitución para encontrar la solución del siguiente sistema de ecuaciones:

${\begin{matrix} 2 x + y = - 1 \\ x - 2 y = - 8 \end{matrix}$

Solución:


Haz Click en los botones para ver los pasos de la Solución

Método de Eliminación

Cuando resolvemos ecuaciones usando el método de eliminación nos valemos de estos dos hechos:

Hecho 1: Si multiplicamos o dividimos ambos lados de una ecuación por una cantidad diferente de cero, la igualdad se mantiene.

Ejemplo Numérico

Ejemplo con Variables

Sabemos que:

8 = 3 + 5

Multiplicando por 2 ambos lados:

2(8) = 2(3 + 5)

16 = 16

Multiplicando por -1 ambos lados:

-1(8) = -1(3 + 5)

-8 = -8

Las siguientes ecuaciones son equivalentes:

	$x + 2 y = 5$
multiplicando por 2 ambos lados	$2 x + 4 y = 10$
multiplicando por -1 ambos lados	$-x - 2 y = -5$

Hecho 2: Si tenemos dos ecuaciones,

a = b

c = d

entonces se cumple que a + c = b + d

Ejemplo Numérico

Ejemplo con Variables

Sabemos que:

6 = 4 + 2

4 = 3 + 1

Sumando los lados correspondientes de la ecuación obtenemos:

6 + 4 = 4 + 2 + 3 + 1

10 = 10

Si tenemos las ecuaciones

$x + 2 y = 5$

$5 x + y = 3$

Entonces,

$x + 2 y + 5 x + y = 5 + 3$

Para resolver un sistema de ecuaciones usando el método de eliminación, seguiremos los siguientes pasos:

Ajustar los coeficientes. Multiplicar ambos lados de una o más ecuaciones por números apropiados, de tal forma que los coeficientes de una de las variables difieran solo en signo.
Sumar los lados correspondientes de las ecuaciones. Esto ocasionará la eliminación de la variable cuyos coeficientes difieren solo en el signo. Resolver para la variable que no fue eliminada.
Sustituir con el valor obtenido. Sustituir el valor de la variable encontrado en el paso anterior en cualquiera de las ecuaciones originales y resolver para la otra variable.
Verificar. Es una buena práctica verificar los resultados para ssegurarnos que no cometimos errores.

Ejemplo 1:

Utilizar el método de Eliminación para encontrar la solución del siguiente sistema de ecuaciones:

${\begin{matrix} x + 2 y = 5 \\ 2 x + 3 y = 8 \end{matrix}$

Solución:


Haz Click en los botones para ver los pasos de la Solución

Ejemplo 2:

Utilizar el método de Eliminación para encontrar la solución del siguiente sistema de ecuaciones:

${\begin{matrix} 4 x - 3 y = 11 \\ 2 x + y = 3 \end{matrix}$

Solución:


Haz Click en los botones para ver los pasos de la Solución

Resumen

Ahora que has completado esta lección, eres capaz de:

Resolver sistemas de ecuaciones lineales por el método de sustitución.
Resolver sistemas de ecuaciones lineales por el método de eliminación.