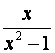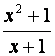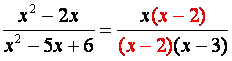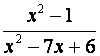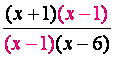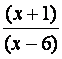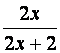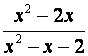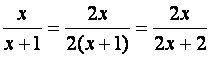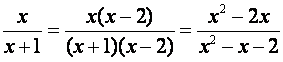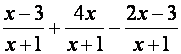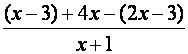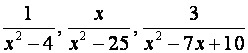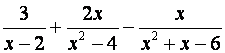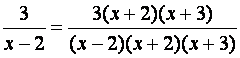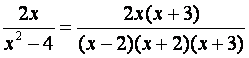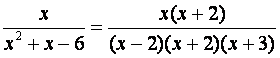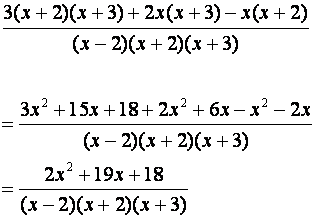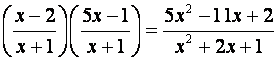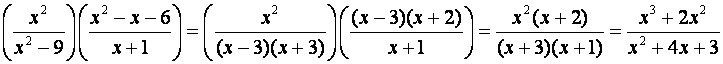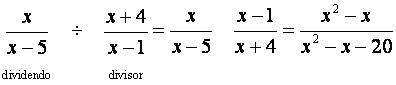Expresiones racionales

Objetivos

Al final de esta lección, debes ser capaz de:

  • Identificar expresiones racionales.
  • Identificar los valores de x donde la gráfica de una fórmula racional cruza el eje de x y dónde no está definida.
  • Simplificar expresiones racionales.
  • Identificar cuándo expresiones racionales son equivalentes
  • Sumar y restar expresiones racionales.
  • Multiplicar y dividir expresiones racionales.

Definición:  Una expresión racional es una de la forma

donde  son polinomios y .   Al igual que en las fracciones numéricas, al polinomio p(x) se le llama el numerador y al polinomio q(x) se le llama el denominador. 

Ejemplo:     

 

 

x es el numerador

  x 2 - 1 es el denominador

 

 

La expresión racional del ejemplo no está definida para los valores donde x es igual a -1 ó 1.




Gráficas de expresiones racionales.

Una fórmula racional tiene la forma

y =
P(x)
______________________________________________
Q(x)
donde P(x) y Q(x) son polinomios.

En la aplicación de abajo, sigue los siguientes pasos:

  1. Mueve los botones para que a = 1, M = 1 y b =- 2
  2. Estas mirando la gráfica
    y =
    x - 1
    ________________________________________
    x + 2
  3. Observa las siguientes características
    • Cuando x = 1, el numerador es igual a cero, lo cual significa que y = 0 y la gráfica está en el eje de x. (El punto esta rotulado A.
    • Cuando x = -2, el denominador es igual a cero, lo cual significa que y no esta definida. (Una línea vertical en x = -2 identifica que no hay ningun valor de y cuando x = -2.


Graficas de expresiones racionales.

Sorry, the GeoGebra Applet could not be started. Please make sure that Java 1.4.2 (or later) is installed and activated. (click here to install Java now)
Usar la aplicación de arriba para hacer las actividades siguientes:
  1. Si
    y =
    x + 1
    ________________________________________
    x + 4
    encuentra los valores de x donde y = 0 y donde y no esta definida.
  2. Si
    y =
    2x + 4
    ________________________________________
    x - 1
    encuentra los valores de x donde y = 0 y donde y no esta definida.
  3. Encuentra una relación racional donde y = 0 cuando x = -3 y donde y no esta definida cuando x = -2.
  4. Encuentra tres relaciones racionales distintas donde y = 0 cuando x = 2 y donde y no está definida cuando x = -4.



Simplificación de expresiones racionales.

Una expresión racional de polinomios está expresada en su forma más simple si no hay factores en común entre los polinomios del numerador y del denominador.

 

Ejemplos 

 

 

Está en su forma más simple.

 

 

No está en su forma más simple.  El factor  es común al numerador y denominador.

 

 

Para simplificarla debemos factorizar el numerador y el denominador.  Luego cancelamos los factores comunes.  Pasamos a ilustrar el procedimiento descrito.

 

Paso 1:  Expresión racional a ser simplificada

 

Paso2:    Ilustración de la factorización del numerador y el denominador y del factor común

Paso3:  Expresión simplificada luego de cancelar factor comunes.

 

Presiona abajo para problemas de simplificar expresiones racionales.

Expresiones racionales equivalentes

Para sumar y restar expresiones racionales, necesitaremos que los denominadores sean iguales.  Esto lo lograremos con el procedimiento para obtener expresiones racionales equivalentes.

 

Ejemplos

 

La expresiones racionales ,  y   son equivalentes. 

 

El procedimiento para obtener expresiones racionales equivalentes a una dada consiste de multiplicar el numerador y el denominador por una misma expresión.  En nuestro ejemplo,  se obtiene multiplicando el numerador y el denominador de  por 2.

 

y se obtiene multiplicando el numerador y el denominador por .

 

 

 

Observación:  Toda expresión racional tiene infinitas expresiones racionales equivalentes.

 




Sumas y Diferencias

 

En la lección de Operaciones con Fracciones, vimos cómo sumar y restar fracciones numéricas. El mismo método se utiliza para sumar y/o restar expresiones racionales de polinomios. Los denominadores tienen que ser iguales. 

  Luego de que esa condición se satisface procedemos a sumar y/o restar las expresiones en el numerador y ese resultado es el numerador de la suma.  El denominador de la suma es el denominador común a todas las expresiones racionales.  Pasamos a ilustrar ese procedimiento con varios ejemplos.

 

Ejemplo 1:  Las expresiones racionales tienen el mismo denominador.

 

Resuelva 

 

 

Paso 1:  Se suman y/o restan todos los numeradores y se escribe sobre el denominador común.

 

 

Paso 2:  Observe que el signo de resta antes del paréntesis le cambia el signo a todos los términos dentro de éste.

 

 

Paso 3:  Sumamos y/o restamos los términos semejantes en el numerador.

 

 

 

 

Para efectuar la suma y/o resta en este caso debemos buscar el denominador común siguiendo el procedimiento:

 

·       Halle la factorización de cada uno de los denominadores

·       Tome el producto de todos los factores distintos que aparezcan considerando la potencia más alta

 

Ejemplo:  Halle el denominador común de las fracciones

 

 

Paso 1:  Factorice cada denominador

 

 

 

Paso 2:  Denominador común

 

Ejemplo 2:  Las expresiones racionales tiene denominadores distintos

Resuelva 

 

 

Paso 1:  Hallar denominador común

 

 

 

Paso 2:  Determine expresiones racionales equivalentes a las dadas

 

 

 

Paso 3:  Sumar los numeradores

 

 

Presione aquí para hacer ejercicios.

 

Presiona abajo para problemas de sumar y restar expresiones racionales.

Multiplicación

 

La multiplicación de expresiones racionales es un procedimiento más sencillo que las operaciones de suma y de resta.  Igual que multiplicar fracciones numéricas que vimos en la lección de Operaciones con Fracciones, para multiplicar expresiones racionales multiplicamos sus respectivos numeradores y sus respectivos denominadores.  Veamos un ejemplo.

 

Ejemplo:

 

 

En los casos en que las expresiones racionales que vamos a multiplicar no estén simplificadas, es conveniente simplificar antes de efectuar la operación. 

 

 

Ejemplo

 

 


Presione para hacer ejercicios de práctica.

 

División

 

Igual que dividir fracciones numéricas que vimos en la lección de Operaciones con Fracciones, la division de expresiones racionales consiste en multiplicar el dividendo por el recíproco del divisor.  Veamos un ejemplo.

 

Ejemplo

 

 

 

Presiona abajo para problemas de multiplicar y dividir expresiones racionales.

Resumen

Ya que has terminado esta lección, debes ser capaz de:

  • Identificar expresiones racionales.
  • Identificar los valores de x donde la gráfica de una fórmula racional cruza el eje de x y dónde no está definida.
  • Simplificar expresiones racionales.
  • Identificar cuando expresiones racionales son equivalentes
  • Sumar y restar expresiones racionales.
  • Multiplicar y dividir expresiones racionales.