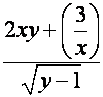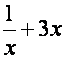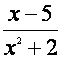Expresiones
Algebraicas y Polinomios
Objetivos
Al final de esta lección, debes ser capaz de:
- Reconocer expresiones algebraicas.
- Reconocer si una expresión algebraica es un polinomio.
- Conseguir el grado y la coeficiente principal de un polinomio.
- Sumar dos polinomios.
- Restar dos polinomios.
Definición:
Una expresión algebraica es un conjunto de cantidades numéricas y literales relacionadas entre sí por los signos de las operaciones aritméticas como sumas, diferencias, multiplicaciones, divisiones, potencias y extracción de raíces.
Algunos ejemplos de expresiones algebraicas son:
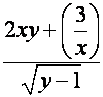 o o 
Si x es una variable, entonces un monomio en x es una expresión de la forma axn, en donde a es un numero real y n es un entero no negativo.
Un binomio es la suma de
dos monomios que no se pueden simplificar y un trinomio es la suma
de tres monomios que no se pueden simplificar.
Recuerda siempre que un monomio tiene solo un término,
un binomio dos términos y un trinomio tres términos.

Polinomios
|
Definición: Un polinomio en x es una suma de la forma:
an xn + an-1 xn-1 + ··· + a2 x2 + a1 x + a0
Donde n es un entero no negativo y cada coeficiente de x es un numero
real. Si an es un numero diferente de cero, se dice que el
polinomio es de grado n.
|
El coeficiente a de la mayor potencia de x es el coeficiente principal del
polinomio.
Ejemplos de polinomios:
|
Ejemplo
|
Coeficiente
principal
|
Grado
|
|
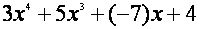
|
3
|
4
|
|
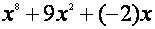
|
1
|
8
|
|
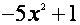
|
-5
|
2
|
|
8
|
8
|
0
|
|
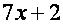
|
7
|
1
|
|
Ejemplos
de expresiones que no son polinomios:
|
a)
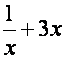 b) b) 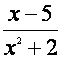 c) c) 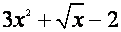
En el primer
ejemplo el exponente de 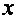 es negativo
contradiciendo la definición de polinomio, de igual forma en el
ejemplo c donde el exponente de es negativo
contradiciendo la definición de polinomio, de igual forma en el
ejemplo c donde el exponente de 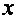 no es entero. no es entero.
En el ejemplo
b tenemos una expresión racional o fraccionaria con un polinomio en el
numerador y otro en el denominador. El criterio que utilizaremos es el
siguiente si el polinomio del denominador no es el constante o de grado cero, la expresión no
es un polinomio. Recuerde que los exponentes deben ser enteros positivos.

Gráficas
Una fórmula polinómica tiene la forma
y = an xn + an-1 xn-1 + ··· + a2 x2 + a1 x + a0.
En la aplicación de abajo, que sigas los siguientes pasos:
- Aprieta la caja que dice lineal para ver la gráfica de un polinomio de grado 1 (una fórmula lineal). Nota que la gráfica cruza el eje de x una vez. El valor de x donde la gráfica cruza el eje de x se llama una raíz o cero de la gráfica. ¿Cuál es la raíz inicial de la gráfica? Juega con los botones para ver como la raíz cambia cuando las coeficientes cambian. Después aprieta la caja que dice lineal de nuevo.
- Aprieta la caja que dice cuadrática para ver la gráfica de un polinomio de orden 2 (una fórmula cuadrática). Mover los botones para que a = 1b = 2 y c = 0. Debes ver que la gráfica tiene dos raíces en x = -1 y x = 0. Mover el botón para que c = 1 y la gráfica tiene solamente una raíz en x = -1. Mueve el botón para que c = 2 y la gráfica no tiene ninguna raíz. Es decir que la gráfica no cruza el eje de x. Un polinomio de orden 2 puede tener 0, 1 o 2 raíces. Juega con los botones para ver como la raíz cambia cuando los coeficientes cambian. Después aprieta la caja que dice cuadrática de nuevo.
- Aprieta la caja que dice cúbica para ver la gráfica de un polinomio de orden 3 (una fórmula cúbica). Un polinomio de orden 3 puede tener 1,2 o 3 raíces. Juega con los botones para ver si puede encontrar coeficientes para que haya 1, 2 y 3 raíces de la gráfica. Después aprieta la caja que dice cúbica de nuevo.
- Aprieta la caja que dice cuártica para ver la grafica de un polinomio de orden 4 (una fórmula cuártica). Un polinomio de orden 4 puede tener 0, 1, 2, 3 o 4 raíces. Juega con los botones para ver si puede encontrar coeficientes para que haya 0, 1, 2, 3 y 4 raíces de la gráfica. Después aprieta la caja que dice cuártica de nuevo.
- Aprieta la caja que dice quíntica para ver la gráfica de un polinomio de grado 5 (una fórmula quíntica). Un polinomio de grado 5 puede tener 1, 2, 3, 4 o 5 raíces. Juega con los botones para ver si puedes encontrar coeficientes para que haya 1, 2, 3, 4 y 5 raíces de la gráfica. Después aprieta la caja que dice quíntica de nuevo.

Suma y Resta de Polinomios:
Suma: Sumamos términos
semejantes es decir sumamos aquellos términos cuyas variables y exponentes
sean iguales. Los pasos para hacer las
suma son:
Paso 1: Elimine los paréntesis
Paso 2. Agrupe términos semejantes
Paso 3. Sume y reste los términos semejantes.
Ejemplo: Halla la suma de:
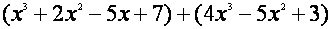

Resta: Funciona igual que la
suma solo hay que tener en cuenta que el signo negativo antes de los
paréntesis cambia el signo de los términos dentro del paréntesis.
Ejemplo: Resta los siguientes
polinomios:
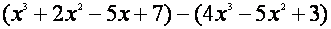
Paso 1: Si un paréntesis tiene antepuesto un signo negativo, los signos dentro del paréntesis se afectan. Los signos se cambian a su opuesto y el signo negativo antepuesto al paréntesis pasa a ser positivo.
Paso 2: Elimine
los paréntesis. Para hacerlo
sólo escriba los términos que están dentro del paréntesis con sus signos
correspondientes e ignore el signo + entre los dos paréntesis.
Paso 3: Agrupe los términos semejantes; es decir los
términos con iguales variables e iguales exponentes.
Paso 4: Sume y reste los términos semejantes.
Así que
aplicando este concepto a la expresión original tendríamos:

Resumen
Ya que has terminado esta lección, debes ser capaz de:
- Reconocer expresiones algebraicas.
- Reconocer si una expresión algebraica es un polinomio.
- Conseguir el grado y el coeficiente principal de un polinomio.
- Sumar dos polinomios.
- Restar dos polinomios.
|