Números Complejos

Objetivos:

Identificar las propiedades de un número complejo
Simplificar raices negativas i
Simplificar potencias de i
Identificar y aplicar las operaciones con números complejos.
Simplificar expresiones con números complejos

Introducción

Si $x^{2} = -1$ entonces $x = \pm \sqrt{-1.}$ Esta ecuación no tiene solución en el conjunto de los números reales ya que si $n$ en un número par $x^{n} ≥
0$ para todo número real. En esta lección se comenzará el estudio de números no reales que provienen de una raíz par de un número negativo.

Definición de Números Imaginarios

Definición:

$\sqrt{- 1} = i$

Normalmente simplificamos números con raices negativas para que sean un número real multiplicado por i.

Ejemplos

$\sqrt{- 16} = \sqrt{16} \times \sqrt{- 1} = \sqrt{16} i = 4 i$
$\sqrt{- 2} = \sqrt{2} \times \sqrt{- 1} = \sqrt{2} i$ Note que la $i$ se encuentra fuera del radical.

Definición

Un número imaginario tiene la forma $b i$ donde b es un número real.

Potencias de i

Para simplificar potencias de i solamente tenemos que recordar que:

$i^{2} = {(\sqrt{- 1})}^{2} = - 1$
${(- 1)}^{n} = 1$ si n es par.
${(- 1)}^{n} = - 1$ si n es impar.

Ejemplos: Expresar los siguientes sin una potencia.

$i^{32} = {(i^{2})}^{16} = {(- 1)}^{16} = 1$
$i^{41} = {(i^{2})}^{20} \times i = {(- 1)}^{20} \times i = 1 \times i = i$
$i^{23} = {(i^{2})}^{11} \times i = {(- 1)}^{11} \times i = - 1 \times i = - i$

Definición de Números Complejos

Definición

Un número complejo tiene la forma $a + b i$ donde a y b son números reales: $a$ se conoce como la parte real y $b$ se conoce como la parte imaginaria.

Ejemplos :

$1 + i$
$3 + \sqrt{2} i$

Para visualizar números complejos, se usa un plano de coordenadas con un eje horizontal para las partes reales y un eje vertical para las partes imaginarias. Cada punto en ese plano llamado el plano complejo corresponde a un número complejo. Mover el punto z en la siguiente aplicación para visualizar números complejos:

Este es un Applet de Java creado con GeoGebra desde www.geogebra.org – Java no parece estar instalado Java en el equipo. Se aconseja dirigirse a www.java.com

Suma y Resta de Complejos

Para sumar dos complejos solo hay que sumar sus partes reales y sus partes imaginarias

: $(a + b i) + (c + d i) = (a + c) + (b + d) i$

Ejemplos

$(1 + 2 i) + (3 + 4 i) = (1 + 3) + (2 + 4) i = 4 + 6 i$
$(1 + 2 i) + (3 - 4 i) = (1 + 3) + (2 - 4) i = 4 - 2 i$
$(1 - 2 i) + (3 - 4 i) = (1 + 3) + (-2 - 4) i = 4 - 6 i$
$(-1 + 2 i) + (3 + 4 i) = (- 1 + 3) + (2 + 4) i = 2 + 6 i$

Para la resta de dos complejos restamos las partes reales y las partes imaginarias $(a + b i) - (c + d i) = (a - c) + (b - d) i$

Ejemplo

$(1 + 2 i) - (3 + 4 i) = (1 - 3) + (2 - 4) i = - 2 - 2 i$
$(1 + 2 i) - (3 - 4 i) = (1 - 3) + (2 + 4) i = - 2 + 6 i$
$(1 - 2 i) - (3 - 4 i) = (1 - 3) + (- 2 + 4) i = - 2 + 2 i$
$(- 1 + 2 i) - (3 + 4 i) = (- 1 - 3) + (2 - 4) i = - 4 - 2 i$

Producto de Complejos

El producto de dos números complejos se hace igual que el producto de expresiones binomiales

Ejemplos

Hallar el producto: $(1 + 2 i) \cdot (3 + 4 i)$

Solución:

$(1 + 2 i) \cdot (3 + 4 i) = 1 \cdot (3 + 4 i) + 2 i \cdot (3 + 4 i) = 3 + 4 i + 6 i + 8 i^{2} = 3 + 10 i + 8 (-1) = - 5 + 10 i$
Hallar el producto: $(2 + i) \cdot (2 + 5 i)$

Solución:
$(2 + i) \cdot (2 + 5 i) = 2 \cdot (2 + 5 i) + i \cdot (2 + 5 i) = 4 + 10 i + 2 i + 5 i^{2} = 4 + 12 i + 5 (-1) = - 1 + 12 i$
Hallar el producto: $(2 - i) \cdot (4 + 3 i)$

Solución:
$(2 - i) \cdot (4 + 3 i) = 2 \cdot (4 + 3 i) - i \cdot (4 + 3 i) = 8 + 6 i - 4 i - 3 i^{2} = 8 + 2 i - 3 (-1) = 11 - 3 i$

Módulo de un Número Complejo.

El valor absoluto o módulo de un número corresponde a la distancia en el plano complejo entre el punto y el origen del plano.

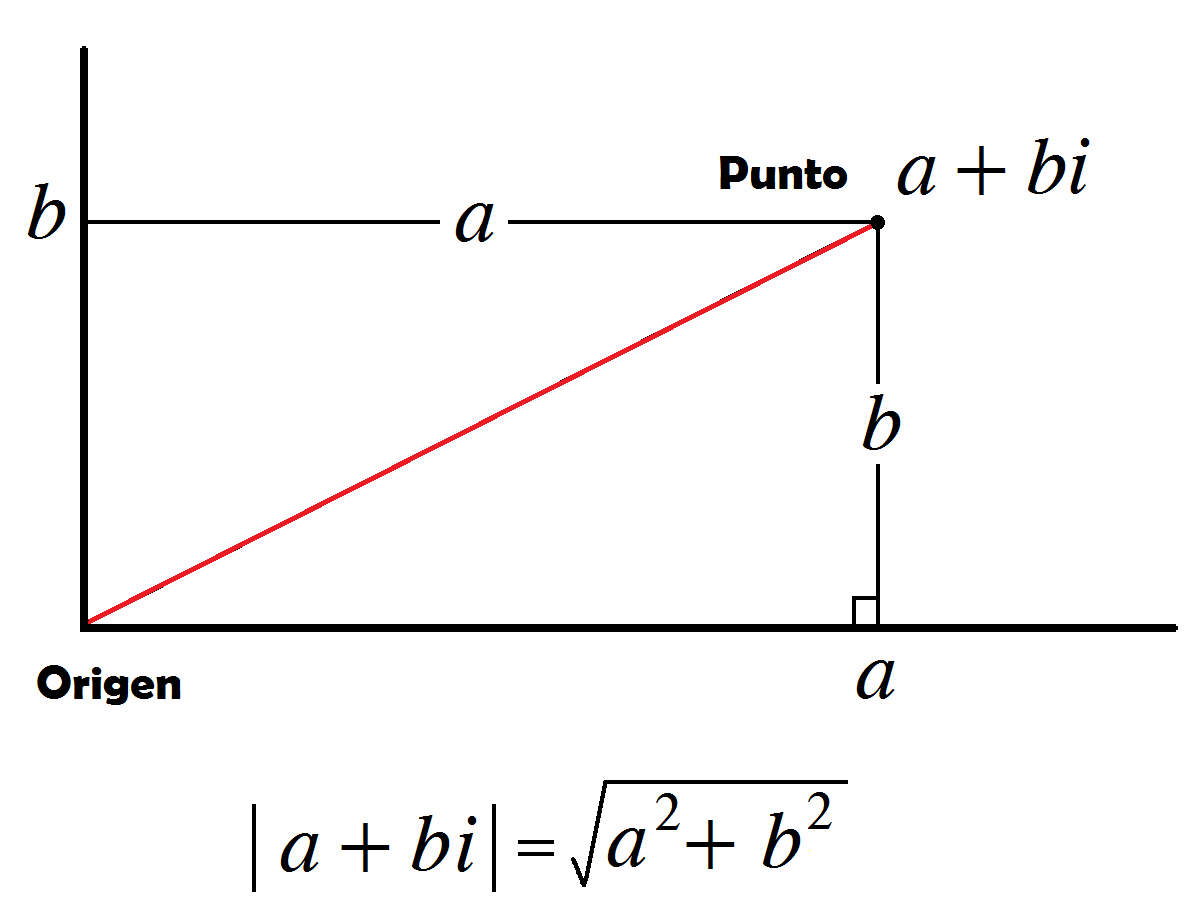
Ejemplos

$| 1 + 3 i | = \sqrt{1^{2} + 3^{2}} = \sqrt{10}$
$| 2 - 3 i | = \sqrt{2^{2} + {(- 3)}^{2}} = \sqrt{13}$
$| 4 - 3 i | = \sqrt{4^{2} + {(- 3)}^{2}} = \sqrt{25} = 5$

Definición: Argumento: El argumento de un número complejo es el ángulo que forma el semieje positivo de abcisas , con la semirrecta que une el origen de coordenadas con su afijo. Dado el número z=a+bi, el argumento de z es: ${θ=tan}^{- 1} (\frac{b}{a})$

Ejemplos

$4 + 2 i = \to θ = \tan^{- 1} (\frac{2}{4}) \to θ = 0.463647609000806$
$5 + 3 i = \to θ = \tan^{- 1} (\frac{3}{5}) \to θ = 0.53704956699803$

Conjugado de un Número Complejo

Para dividir dos números complejos necesitamos definir lo que es el conjugado de un número complejo

Definición

Sea $z$ un número complejo de la forma $z = a + b i$ , llamaremos el conjugado de $z$ al número complejo de la forma $\bar{z} = \bar{a + b i} = a - b i$

Ejemplos

$\bar{3 + 4 i} = 3 - 4 i$	$\bar{2 - 5 i} = 2 + 5 i$

$\bar{- 3 i} = 3 i$	$\bar{- 4} = - 4$

Nota: Multiplicando un número complejo con su conjugado da el módulo cuadrado.

$(3 + 4 i) \cdot \bar{3 + 4 i} = 3^{2} + 4^{2}$
$(3 - 5 i) \cdot \bar{2 - 5 i} = 3^{2} + 5^{2}$
$(a + b i) \cdot \bar{a + b i} = a^{2} + b^{2}$

División de Complejos

Para el cociente de dos números complejos es encesario introducir una nueva terminología, la cual es muy útil al momento de dividir números complejos, sin embargo iniciemos viendo como seria la division de un complejo sobre un real. Para dividir un complejo sobre un real se hace lo siguiente : $\frac{a + b i}{r} = \frac{a}{r} + \frac{b}{r} i$ . Veamos el siguiente ejemplo:

Ejemplo

$\frac{2 + 3 i}{2} = \frac{2}{2} + \frac{3}{2} i = 1 + \frac{3}{2} i$

El conjugado nos permite cambiar dividir por un número complejo a multiplicar por un número complejo y dividir por un número real:

$\frac{a + b i}{c + d i} = \frac{(a + b i) \bar{(c + d i)}}{(c + d i) \bar{(c + d i)}} = \frac{(a + b i) (c - d i)}{(c + d i) (c - d i)} = \frac{(a c + b d) + (b c - a d) i}{c^{2} + d^{2}} = \frac{(a c + b d)}{c^{2} + d^{2}} + \frac{(b c - a d)}{c^{2} + d^{2}} i$

Ejemplos

$\frac{1 + 2 i}{3 + 4 i} = \frac{1 + 2 i}{3 + 4 i} \cdot \frac{3 - 4 i}{3 - 4 i} = \frac{(1 + 2 i) (3 - 4 i)}{(3 + 4 i) (3 - 4 i)} = \frac{3 - 4 i + 6 i - 8 i^{2}}{9 - 16 i^{2}} = \frac{3 - 4 i + 6 i - 8 (-1)}{9 - 16 (-1)} = \frac{3 + 8}{9 + 16} + \frac{6 - 4}{9 + 16} i = \frac{11}{25} + \frac{2}{25} i$
$\frac{3 + i}{1 - 6 i} = \frac{3 + i}{1 - 6 i} \cdot \frac{1 + 6 i}{1 + 6 i} = \frac{(3 + i) (1 + 6 i)}{(1 - 6 i) (1 + 6 i)} = \frac{3 + 18 i + i + 6 i^{2}}{1 - 36 i^{2}} = \frac{3 + 18 i + i + 6 (-1)}{1 - 36 (-1)} = \frac{3 - 6}{1 + 37} + \frac{18 + 1}{1 + 37} i = - \frac{3}{37} + \frac{19}{37} i$

Resumen

Ahora que terminaste la lección, eres capaz de:

Identificar las propiedades de un número complejo
Simplificar raices negativas i
Simplificar potencias de i
Identificar y aplicar las operaciones con números complejos.
Simplificar expresiones con números complejos

Objetivos:

Introducción

Definición de Números Imaginarios

Un número imaginario tiene la forma b i donde b es un número real.

Potencias de i

Definición de Números Complejos

Un número complejo tiene la forma a+ b i donde a y b son números reales: a se conoce como la parte real y b se conoce como la parte imaginaria.

Suma y Resta de Complejos

Producto de Complejos

Módulo de un Número Complejo.

Conjugado de un Número Complejo

Sea z un número complejo de la forma z = a + b i , llamaremos el conjugado de z al número complejo de la forma z ¯ = a + b i ¯ = a - b i

Nota: Multiplicando un número complejo con su conjugado da el módulo cuadrado.

División de Complejos

Resumen

Un número imaginario tiene la forma $b i$ donde b es un número real.

Un número complejo tiene la forma $a + b i$ donde a y b son números reales: $a$ se conoce como la parte real y $b$ se conoce como la parte imaginaria.

Sea $z$ un número complejo de la forma $z = a + b i$ , llamaremos el conjugado de $z$ al número complejo de la forma $\bar{z} = \bar{a + b i} = a - b i$