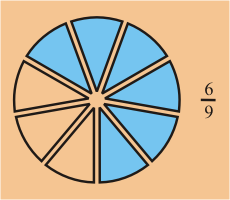
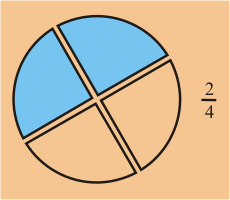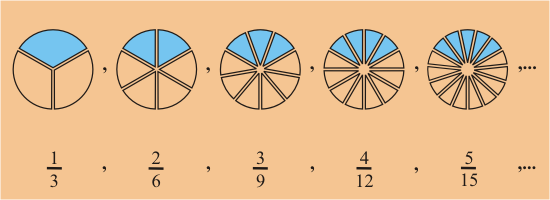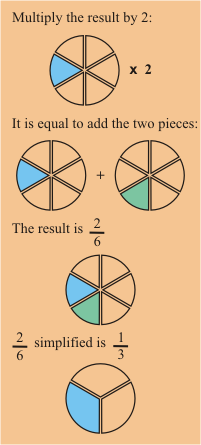Numerador y Denominador
Una fracción tiene dos números organizados verticalmente con una
línea entre ellos. El número de arriba es llamado el numerador y el número de abajo es el denominador.
Significado del Denominador
El denominador de una fracción hace referencia al número de partes iguales en las que un conjunto ha sido dividido. Por ejemplo, si tenemos un pastel y lo dividimos en dos partes, nuestra fracción asociada contiene 2 en el denominador.
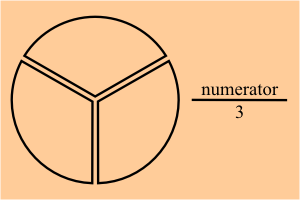
Si dividimos nuestro pastel en tres pedazos, nuestra fracción asociada contiene 3 en el denominador.
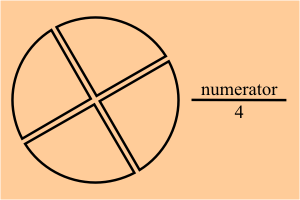
Si dividimos nuestro pastel en cuatro pedazos, nuestra fracción asociada
contienen 4 en el denominador.
Significado del Numerador
Hemos aprendido que el denominador de una fracción se refiere al número de partes en las que la cantidad total se ha dividido. El numerador de una fracción se refiere al número de estas partes que tomamos.
Por ejemplo, si dividimos un pastel en cuatro pedazos, nuestra fracción asociadas contiene 4 en
el denominador para indicar que hemos dividido el pastel en cuatro pedazos. Si tenemos tres de estas partes, nuestro numerador
contendrá el 3.
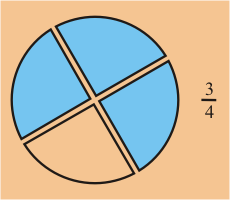
Si nosotros dividimos el pastel en 3 partes, la fracción asociada que contiene
el 3 en el denominador indica que nosotros hemos dividido el pastel en tres partes. Si tomamos dos de esas partes,
nuestro numerador contendra el 2.
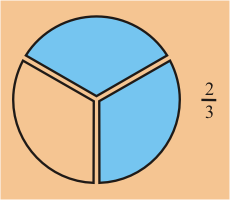
Haz clic aquí para visualizar la práctica la relación entre numeradores, denominadores y la fracción asociada.

Haz clic a continuación para obtener una práctica visual de la fracción correcta de un entero.

Fracciones Equivalentes
Dado un Pastel, podemos usar el significado de numerador y denominador para obtener la cantidad
asociada con las siguientes fracciones.
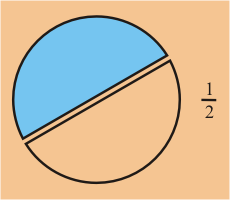
Podemos ver que estas fracciones hacen referencia a la misma cantidad.
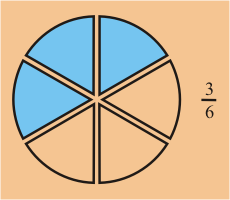
Dada una fracción, podemos usar el significado del numerador y denominador para obtener
las cantidades asociadas con las siguientes fracciones
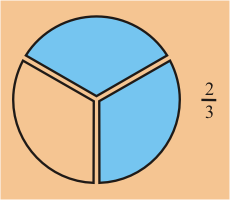
Una vez más, podemos ver que estas fracciones hacen referencia a una misma cantidad.
Puesto que
hace referencia a dos enteros, vale la pena señalar que los
números enteros tienen forma fraccionaria.
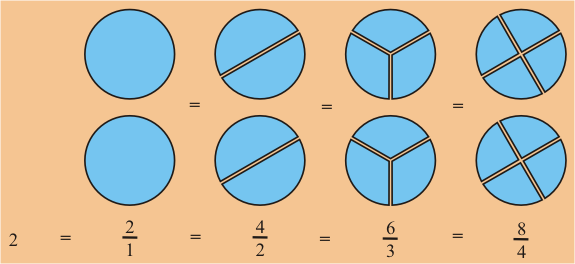
Fracciones en Forma Reducida
Hemos visto que hay muchas maneras de expresar la misma cantidad con fracciones. Teniendo en cuenta todas las representaciones posibles de una cantidad, si seleccionamos la fracción donde el numerador y denominador tienen los valores más pequeños posibles, la fracción se dice que es en forma reducida.
Por ejemplo: Dado
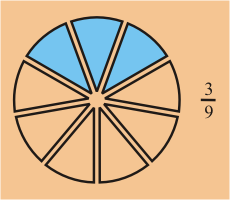
Podemos expresar esta cantidad con las siguientes fracciones.
Así, la fracción en su forma más simple sería .
Práctica:
Suma de Fracciones
No hay ningún problema sumando partes del mismo tamaño.
Es decir, dos fracciones con el mismo denominador.
Ejemplo:

Ejemplo:

Si las partes son de diferentes tamaños, son un poco más difíciles de sumar.
Ejemplo:

Podemos ver la cantidad que se muestra en esta suma con mucha facilidad,
sin embargo expresar la suma es más difícil.

Si recordamos las fracciones se pueden expresar en muchas formas, sin embargo, podemos solucionar este problema.
Solución para :
-
Expandir las dos fracciones utilizando los denominadores adecuados.
-
Seleccione el denominador común más pequeño de estas dos expansiones
y exprese las fracciones en términos de su "minimo común denominador".
 ,
, 
-
Ahora que los dos denominadores son iguales, las dos fracciones se pueden sumar.
Practica:
Resta de Fracciones
No hay ningún problema al restar partes del mismo tamaño. Es decir, dos fracciones con el mismo denominador. Por ejemplo
Ejemplo:
Si las partes son de diferentes tamaños, son un poco más difíciles de restar. Por ejemplo
Podemos ver la cantidad que se muestra en esta diferencia con mucha facilidad, sin embargo expresar la resta es más difícil.
Una vez más, si tenemos en cuenta que las fracciones se pueden expresar de muchas maneras, se puede solucionar este problema.
Solución para :
-
Expandir las dos fracciones utilizando los denominadores adecuados.
-
Seleccione el denominador común más pequeño de estas dos expansiones
y exprese las fracciones en términos de su "minimo común denominador".
 ,
, 
-
Ahora que los dos denominadores son iguales,
las dos fracciones se pueden restar.
Multiplicación de Fracciones
Si multiplicamos una cantidad por una fracción , donde indica que vamos a dividir la cantidad en partes y luego se multiplica esto por el numerador .
Por ejemplo: significa que primero tomamos un tercio de la mitad.

El resultado de esto es . A continuación, multiplicamos el resultado por 2.
Por lo tanto .
Por ejemplo: significa que primero tomamos un medio de dos tercios

El resultado de esto es una tercera parte que luego se multiplica por 3.

Por lo tanto .
Observando estos ejemplos, nos encontramos con que un enfoque práctico para esto puede ser .
División de Fracciones
En la sección anterior vimos que multiplicar por es lo mismo que dividir por 2. También, que la multiplicación por es lo mismo que dividir por 3. En general, multiplicar por es lo mismo que dividir por . Por lo tanto, si dividimos una cantidad por una fracción sólo necesitamos intercambiar y y multiplicar.
Más simplemente, .
Por ejemplo: .
Practica: