Graficando en un sistema de coordenadas cartesianas

Objetivos

Al concluir esta lección, deberás ser capaz de:

Graficar un punto (a,b) en el plano cartesiano.
Identificar cualquier punto en el plano cartesiano usando coordenadas (x,y).
Encontrar el punto medio de dos puntos.

Coordenadas en la recta numérica real

La recta numérica real organiza puntos alrededor de un punto llamado cero. Cada número o punto en la recta contiene dos elementos.

El signo del número indica si el número se encuentra a la izquierda o la derecha del cero. Los números positivos se encuentran a la derecha del cero. Los números negativos se encuentran a la izquierda del cero.
El valor absoluto de un número indica la distancia desde cero hasta el punto.

Ejemplo:

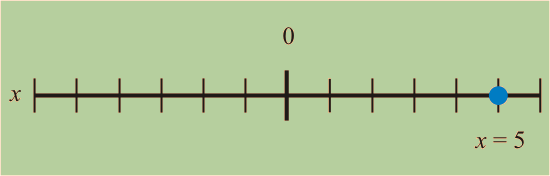
Encuentra el punto que corresponde al número x = 5 en la recta numérica.

Solución:

El signo del 5 es positivo, por lo tanto el número se encuentra a la derecha del cero.
El valor absoluto del número es 5, lo cual indica que la distancia desde cero es 5 unidades.

Usando estos dos datos, podemos colocar el punto x=5 en la siguiente recta numérica.

Ejemplo:

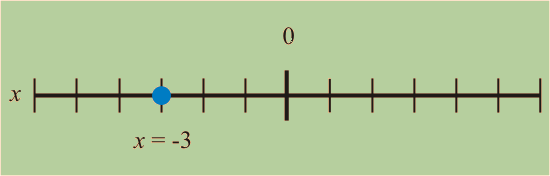
Encuentra el punto que corresponde al número x = -3 en la recta numérica.

Solución:

El signo de -3 es negativo, por lo tanto el número se encuentra a la izquierda del cero.

El valor absoluto del número es 3, lo cual indica que la distancia desde cero es 3 unidades.

Usando estos dos datos, podemos colocar el punto x= -3 en la siguiente recta numérica.

Para ver otros puntos en la recta numérica, presiona el botón asociado con el valor de x al cual quieras ver.

Ahora, practica al presionar la recta numérica en el valor indicado de x.

Si la recta numérica real es orientada verticalmente, los dos elementos de un número y, en esta recta vertical son como sigue.

El signo del número indica si el número se encuentra arriba o abajo del cero. Los números positivos están sobre cero. Los números negativos están bajo cero.

El valor absoluto del número indica la distancia desde cero.

¡Practica este concepto en la aplicación que se muestra abajo!

El sistema de coordenadas cartesianas

El sistema de coordenadas cartesianas combina la recta numérica de x y la recta numérica de y. Si comenzamos al centro de nuestra cuadrícula, en el punto llamado origen, el valor para x es el número de unidades a la izquierda/derecha que nos movamos. El valor para y es el número de unidades arriba y abajo que nos movamos. Usando x y y juntos, podemos obtener cualquier localización o punto (x,y) en el plano cartesiano. Presione en cualquier punto para ver las coordenadas (x,y) asociadas al punto.

En el ejemplo de arriba, vimos las coordenadas (x,y) cuando tanto x como y son enteros. De hecho, no hay necesidad estos tengan que asumir valores enteros. Presione en cualquier punto para ver las coordenadas (x,y) asociadas al punto.

Es hora de demostrar que lo entendiste. Intenta tu mismo presionando el punto asociado con los valores de x y y dados.

Oprime el siguiente botón para practicar identificando las coordenadas asociadas con un punto:

Punto Medio
Dados dos puntos, saber encontrar el punto medio es muy útil. Por ejemplo, suponga que se nos proveen dos puntos opuestos sobre una circunferencia. Con la información de estos dos puntos podríamos encontrar el centro del círculo, claro está necesitamos conocer comó encontrar el punto medio para esto. Podemos definir el punto medio entre dos puntos de la recta real de la siguiente manera.

Punto Medio en la Recta Real

Sean a y b dos puntos de la recta real con valores $x_{1}$ y $x_{2}$ respectivamente. El punto medio entre ellos viene dado por la siguiente fórmula:
$P_{M} = \frac{x_{1} + x_{2}}{2}$

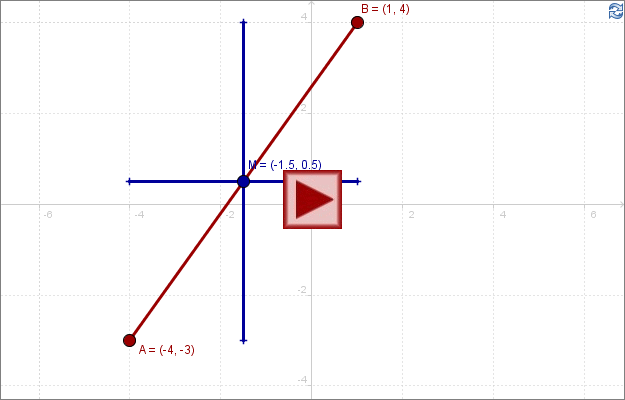
La siguiente aplicación interactiva te permitirá investigar el punto medio entre dos puntos. Mueve los puntos a y b para ver como cambia el punto medio.

Ejercicio: En la siguiente aplicación, mueva el punto a hasta que su valor sea a = 1. Después, mueva el punto b hasta que su valor sea b = 5. Si calculamos el punto medio este viene dado por: $P_{M} = \frac{1 + 5}{2} = \frac{6}{2} = 3$
Este es precisamente el valor indicado por el punto m en la aplicación anterior. Puedes construir cuantos ejemplos sean necesarios para entender el concepto.
This is a Java Applet created using GeoGebra from www.geogebra.org - it looks like you don't have Java installed, please go to www.java.com

Jesús M. Cajigas, Created with GeoGebra

Es una buena estrategia construir tus ejemplos en una hoja de papel, resolverlos y finalmente corroborar tu resultado utilizando la aplicación anterior.
Como ya conocemos como encontrar el punto medio para dos puntos en la recta real podemos discutir como encontrar el punto medio para dos puntos en el plano cartesiano. Como el plano cartesiano es formado por la intersección de dos rectas reales tiene sentido pensar que para encontrar el punto medio para dos puntos en el plano cartesiano debemos hacer el proceso descrito anteriormente dos veces. Podemos definir el punto medio entre dos puntos del plano cartesiano de la siguiente manera.

Punto Medio en el Plano Cartesiano

Sean A y B dos puntos de la recta real con coordenadas $(x_{1}, y_{1})$ y $(x_{2}, y_{2})$ respectivamente. El punto medio entre ellos viene dado por la siguiente fórmula:
$P_{M} = (\frac{x_{1} + x_{2}}{2}, \frac{y_{1} + y_{2}}{2})$

La siguiente aplicación interactiva te permitirá investigar el punto medio entre dos puntos. Mueve los puntos A y B para ver como cambia el punto medio.

Ejercicio: En la siguiente aplicación, mueva el punto A hasta que sus coordenadas sean (1,1). Ahora, mueva el punto B hasta que sus coordenadas sean (5,3). Calculemos el punto medio para utilizando los puntos anteriores. $P_{M} = (\frac{1 + 5}{2}, \frac{1 + 3}{2}) = (\frac{6}{2}, \frac{4}{2}) = (3, 2)$ Asi pues el punto medio entre A y B tiene coordenadas (3,2). Este valor es el que aparece indicado en nuestra aplicación como el punto M.

Al igual que en la aplicación anterior puedes hacer cuantos ejemplos consideres necesario para entender el concepto. Puedes tan solo investigar con la aplicación o utilizarla para corroborar ejercicios que hagas por tu cuenta en una hoja de papel.
Es importante recordar los siguientes puntos:

El punto medio, ya sea en la recta real o en el plano cartesiano, debe expresarse con la notación correcta con la que se escriben los puntos en el plano o en la recta.

Es de vital importancia que etiquetes de manera correcta las corrdenadas de cada punto. Es decir, si A tiene coordenadas (1,2) y decimos que $(x_{1} = 1)$ no podemos decir que $(y_{2} = 2)$ debemos decir $(y_{1} = 2)$ . Debe haber una correspondencia entre los índices de cada coordenada.

Finalmente, no confunda las coordenadas en x con las de y. La primera coordenada en cualquier par ordenado corresponde a x y la segunda a y.

Aplicación Interactiva
Las siguientes aplicaciones interactivas te permitirán ver un poco del uso de los planos cartesianos. Para ser mas preciso te permitiran trabajar con un mapa de huracanes. Diviertete mientras manejas el huracan Iris y entiendes la utilidad y necesidad de un plano cartesiano. Para comenzar cualquiera de las aplicaciones haz click en el botón correspondiente.

Resumen

Ya que has terminado con esta lección, debes poder:

Graficar un punto (a,b) en el plano cartesiano.

Identificar cualquier punto en el plano cartesiano usando coordenadas (x,y).

Encontrar el punto medio de dos puntos.