Objetivos:
Al terminar esta
experiencia el estudiante podrá
1. Describir la gráfica de funciones de la
forma ![]() , con
, con ![]() en términos de traslaciones horizontales, traslaciones verticales,
estiramientos, contracciones y reflexiones de la función cuadrática básica
en términos de traslaciones horizontales, traslaciones verticales,
estiramientos, contracciones y reflexiones de la función cuadrática básica
2. Construir la fórmula de una función
cuadrática que ha sido descrita en términos de traslaciones.
3. Determinar el vértice, eje de simetría, interceptos en los ejes, interceptos
con rectas horizontales, concavidad, y valores extremos de la gráfica de
funciones cuadráticas.
4. Completar el cuadrado para reescribir
una reescribir una función cuadrática descrita en la forma
general ![]() en la forma canónica equivalente
en la forma canónica equivalente ![]() .
.
5. Encontrar la forma canónica de una
función cuadrática cuando sabemos información sobre su gráfica.
6. Trazar la gráfica de una función
cuadrática escrita en la forma general ![]()
Sabemos que la
gráfica de la función cuadrática básica ![]() corresponde a una parábola que abre
hacia arriba, tiene vértice en el origen, pasa por el punto
corresponde a una parábola que abre
hacia arriba, tiene vértice en el origen, pasa por el punto ![]() y
exhibe simetría con respecto al eje de
y
exhibe simetría con respecto al eje de ![]() Podemos estudiar transformaciones de la gráfica de esta función
considerando la función
Podemos estudiar transformaciones de la gráfica de esta función
considerando la función![]() , donde
, donde ![]() son números reales y
son números reales y ![]() . Nota que si escogemos los valores
. Nota que si escogemos los valores ![]() obtenemos la función cuadrática básica.
obtenemos la función cuadrática básica.
En esta experiencia
explorarás las propiedades de funciones de la forma![]() , con
, con ![]() En
la aplicación siguiente utilizarás los deslizadores para sistemáticamente
modificar los valores de los parámetros
En
la aplicación siguiente utilizarás los deslizadores para sistemáticamente
modificar los valores de los parámetros ![]() y
estudiar los cambios que ocurren en la gráfica.
y
estudiar los cambios que ocurren en la gráfica.
(A mi juicio El applet disponible en la siguiente página electrónica es muy
apropiado para investigar el rol de a, h y k)
Se utilizará en las actividades 1 a 4
Actividad 1 El rol del parámetro ![]()
Mueve los deslizadores en la aplicación de forma que ![]() .
.
¡Mantén
constantes los valores de ![]() y
y ![]() !
!
Traza la gráfica
de ![]() para los valores
para los valores ![]() . Compara la gráfica resultante con la
gráfica de la función cuadrática básica
. Compara la gráfica resultante con la
gráfica de la función cuadrática básica ![]() . ¿Que podemos decir de la gráfica de
. ¿Que podemos decir de la gráfica de ![]()
Traza la gráfica
de ![]() para los valores
para los valores ![]() . ¿Qué podemos decir de la gráfica de
. ¿Qué podemos decir de la gráfica de ![]()
Actividad 2 El rol del parámetro ![]()
En esta
experiencia explorarás el efecto de cambiar el valor del parámetro![]() en funciones de la forma
en funciones de la forma![]() .
.
Mueve los deslizadores en la aplicación siguiente de
forma que ![]() .
.
¡Mantén
constantes los valores de ![]() y
y
![]() !
!
Explora la
gráfica de ![]() para los valores
para los valores ![]() . ¿Que efecto tiene cambiar el valor de
. ¿Que efecto tiene cambiar el valor de ![]() ?
?
Explora la gráfica de ![]() para los valores
para los valores ![]() .
.
Actividad 3 El rol del parámetro ![]()
En esta
experiencia explorarás las propiedades de funciones de la forma![]() , con
, con ![]()
Mueve los deslizadores en la aplicación siguiente de
forma que ![]() .
.
¡Mantén constantes los valores de ![]() y
y ![]() !
!
1. Traza la gráfica de ![]() para los valores
para los valores ![]() .
¿Qué efecto tiene cambiar el valor de
.
¿Qué efecto tiene cambiar el valor de ![]() ?
?
2. Traza la gráfica de ![]() para los valores
para los valores ![]() .
¿Qué efecto tiene usar valores de
.
¿Qué efecto tiene usar valores de ![]() tal que
tal que ![]() ?
?
3. Traza la gráfica de ![]() para los valores a=
para los valores a=![]() .
¿Qué efecto tiene usar valores de
.
¿Qué efecto tiene usar valores de ![]() tal que
tal que ![]() ?
?
La gráfica de ![]() , puede obtenerse de la gráfica de
, puede obtenerse de la gráfica de ![]() , mediante una sucesión de
transformaciones
, mediante una sucesión de
transformaciones
·
una
traslación horizontal de la gráfica de![]()
·
seguida
por un estiramiento, contracción o
reflexión vertical de la gráfica
resultante,
·
una traslación vertical
El valor del
parámetro ![]() , determina la traslación horizontal, el
valor de
, determina la traslación horizontal, el
valor de ![]() determina si realizaremos un estiramiento,contracción o reflexión de la gráfica resultante, el valor
de
determina si realizaremos un estiramiento,contracción o reflexión de la gráfica resultante, el valor
de ![]() indica la presencia de una traslación
vertical.
indica la presencia de una traslación
vertical.
Actividad 4
En cada
problema a continuación, construye la
fórmula de la función que se obtiene al
trasformar la gráfica de ![]() en la forma descrita. Usa la
a aplicación para verificar tu respuesta.
Para provocar cambios en la gráfica debes modificar los valores de los parámetros
en la forma descrita. Usa la
a aplicación para verificar tu respuesta.
Para provocar cambios en la gráfica debes modificar los valores de los parámetros ![]() moviendo los deslizadores de la
aplicación.
moviendo los deslizadores de la
aplicación.
1. Traslación 2 unidades hacia la derecha y
3 unidades hacia arriba.
2. Traslación 3 unidades a la izquierda y 2
hacia arriba.
3. Traslación 2 unidades a la izquierda,
reflexión con respecto al eje de x, 1 unidad hacia arriba.
4. Traslación 2 unidad a la derecha, 1 unidad hacia arriba, seguida por una reflexión
con respecto al eje de x.
5. Estiramiento por un factor de 3,
traslación 1 a la derecha , traslación 2 unidades hacia abajo
La gráfica de ![]() es una parábola con vértice en
es una parábola con vértice en ![]() La recta vertical que pasa por el vértice es
su eje de simetría. Cuándo
La recta vertical que pasa por el vértice es
su eje de simetría. Cuándo ![]() , la parábola abre hacia arriba. Más aun,
tenemos
, la parábola abre hacia arriba. Más aun,
tenemos ![]() para todos los valores de
para todos los valores de ![]() .
Por lo que,
.
Por lo que, ![]() para toda
para toda ![]() .
Es decir,
.
Es decir, ![]() asume el valor mínimo global de
asume el valor mínimo global de ![]() , cuando
, cuando ![]() De modo que el punto más bajo de la gráfica de
De modo que el punto más bajo de la gráfica de ![]() es el vértice de la parábola. En caso de que
es el vértice de la parábola. En caso de que ![]() , la parábola abre hacia abajo y el
valor de
, la parábola abre hacia abajo y el
valor de ![]() del vértice de la parábola es el valor máximo
global de
del vértice de la parábola es el valor máximo
global de ![]()
Actividad 5
Considera la función
![]() . Llena los blancos (interactivo)
. Llena los blancos (interactivo)
1. Podemos obtener la gráfica de ![]() trasladando horizontalmente la gráfica de
trasladando horizontalmente la gráfica de ![]() _____________unidad a la ______________. Estirando la gráfica resultante por un factor
de ____________, y trasladando verticalmente esta gráfica ________ unidades
hacia abajo. Bajo esta transformación el
punto (-3,9) sobre la gráfica de
_____________unidad a la ______________. Estirando la gráfica resultante por un factor
de ____________, y trasladando verticalmente esta gráfica ________ unidades
hacia abajo. Bajo esta transformación el
punto (-3,9) sobre la gráfica de ![]() es enviado al punto ______________ sobre la gráfica de
es enviado al punto ______________ sobre la gráfica de ![]()
2. La gráfica de ![]() es una _________________ simétrica a la recta
___________ . Por inspección sabemos que
es una _________________ simétrica a la recta
___________ . Por inspección sabemos que ![]() , la simetría de la gráfica asegura que
otro valor de
, la simetría de la gráfica asegura que
otro valor de ![]() , también satisface
, también satisface ![]() ¿Cuál es?___________________
¿Cuál es?___________________
3. Como
el vértice está en el
punto ____________, y la curva abre hacia _________ , el
campo de valores de esta función es el intervalo _______________. Es decir, ![]() para
todos los valores de
para
todos los valores de ![]() .
Esto implica que
.
Esto implica que ![]() asume un valor __________ de _______ cuando
asume un valor __________ de _______ cuando ![]() .
.
4. La curva corta el eje de ![]() en el punto _____________. En cuántos puntos
la gráfica de
en el punto _____________. En cuántos puntos
la gráfica de ![]() corta el eje de
corta el eje de ![]() ? ¿Por qué?
? ¿Por qué?
5. La gráfica corta el eje de ![]() en _________________.
en _________________.
6. Además ![]() cuando
cuando ![]() o
o
![]() .
.
7. Al expandir la función ![]() -3, obtenemos una expresión equivalente
en la forma
-3, obtenemos una expresión equivalente
en la forma ![]() .
¿Cuáles
son los valores de
.
¿Cuáles
son los valores de ![]() ____________________.
____________________.
Respuestas
1. Podemos obtener la gráfica de ![]() trasladando horizontalmente la gráfica de
trasladando horizontalmente la gráfica de ![]() una
unidad a la izquierda . Estirando la gráfica resultante por un factor
de 2, y trasladando verticalmente esta gráfica 3 unidades hacia
abajo. Bajo esta transformación el punto
(-3,9) sobre la gráfica de
una
unidad a la izquierda . Estirando la gráfica resultante por un factor
de 2, y trasladando verticalmente esta gráfica 3 unidades hacia
abajo. Bajo esta transformación el punto
(-3,9) sobre la gráfica de ![]() es enviado al punto__
es enviado al punto__![]() sobre la gráfica de
sobre la gráfica de ![]()
2. La gráfica de ![]() es una parábola simétrica a la recta x=-1.
Por inspección sabemos que
es una parábola simétrica a la recta x=-1.
Por inspección sabemos que ![]() , la simetría de la gráfica asegura que
otro valor de
, la simetría de la gráfica asegura que
otro valor de ![]() , también satisface
, también satisface ![]() ¿Cuál es ese valor ?
¿Cuál es ese valor ?
![]() .
.
3. Como el
vértice está en el punto ![]() , y la curva abre hacia arriba , el campo de valores de esta función es el
intervalo _
, y la curva abre hacia arriba , el campo de valores de esta función es el
intervalo _![]() . Es decir,
. Es decir, ![]() para todos los valores de
para todos los valores de ![]() .
Esto implica que
.
Esto implica que ![]() asume un valor ___mínimo de 3 cuando
asume un valor ___mínimo de 3 cuando ![]() .
.
4. La curva corta el eje de ![]() en el punto
en el punto ![]() . ¿En cuántos puntos la gráfica de
. ¿En cuántos puntos la gráfica de ![]() corta el eje de
corta el eje de ![]() ?
¿Por qué? La gráfica corta el eje de
?
¿Por qué? La gráfica corta el eje de ![]() en dos puntos, puesto que a parábola abre hacia arriba y el vértice
está por debajo del eje de
en dos puntos, puesto que a parábola abre hacia arriba y el vértice
está por debajo del eje de ![]()
5. La gráfica corta el eje de ![]() en los puntos
en los puntos 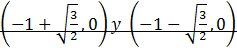 _.
_.
6. Además ![]() cuando
cuando ![]() o
o
![]() .
.
7. Al expandir la función ![]() -3, obtenemos una expresión equivalente
en la forma
-3, obtenemos una expresión equivalente
en la forma ![]() .
¿Cuáles
son los valores de
.
¿Cuáles
son los valores de ![]() .
.
La
estrategia de completar el cuadrado permite reescribir una función cuadráica
descrita en la forma general ![]() en la forma canónica equivalente
en la forma canónica equivalente ![]() . Esto
garantiza que la gráfica de todo polinomio de segundo grado corresponda a una
parábola, cuyo vértice, eje de simetría,
valores máximo y mínimo podemos determinar fácilmente.
. Esto
garantiza que la gráfica de todo polinomio de segundo grado corresponda a una
parábola, cuyo vértice, eje de simetría,
valores máximo y mínimo podemos determinar fácilmente.
Practica este
proceso con los problemas sugeridos por la siguiente aplicación:
Actividad 6
(Me gusta
mucho esta aplicación. El único problema
es que periódicamente produce “nuevas parábolas” de la forma y=-1, y=2……)
Actividad 7 ( Tarea de laboratorio)
Contesta cada una de las siguientes preguntas. Usa la a aplicación
para verificar tu
respuesta. Para provocar cambios en la
gráfica debes modificar los valores de los parámetros ![]() moviendo los deslizadores de la
aplicación. Si fuera necesario puedes controlar el largo y el
incremento de los valores de cada parámetro dando un clic sobre la letra correspondiente.
moviendo los deslizadores de la
aplicación. Si fuera necesario puedes controlar el largo y el
incremento de los valores de cada parámetro dando un clic sobre la letra correspondiente.
Encuentra
una fórmula para ![]() , si la gráfica de
, si la gráfica de ![]() es una parábola que …
es una parábola que …
1. …pasa por el punto ![]() y tiene
vértice en el punto
y tiene
vértice en el punto ![]() .
.
2. … toma el valor máximo de 3, es
simétrica a la recta![]() y
tiene intercepto en
y
tiene intercepto en ![]() igual a
igual a ![]() .
.
3. …corta el eje de ![]() cuando
cuando ![]() y
y ![]() y
valor mínimo -3.
y
valor mínimo -3.
4. …pasa por los punto ![]() y
y
![]() y
es simétríca a la recta
y
es simétríca a la recta ![]() ,
,
5. ![]() ….pasa por el origen, por el punto
….pasa por el origen, por el punto ![]() ) y el punto
) y el punto ![]()
6. ….pasa por el origen, por el punto ![]() , y el punto
, y el punto ![]() .
.
Actividad 8
El siguiente enlace trabaja varias
de las ideas que hemos trabajado en esta unidad. Puedes visitarlo para repasar las ideas que
has aprendido desde otro punto de vista.
Éxito!
| Graphing Quadratic Functions | |
|
f(x) = ax^2 + bx + c
( x , y ) |
|