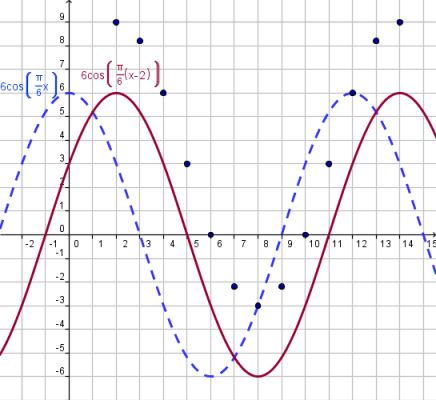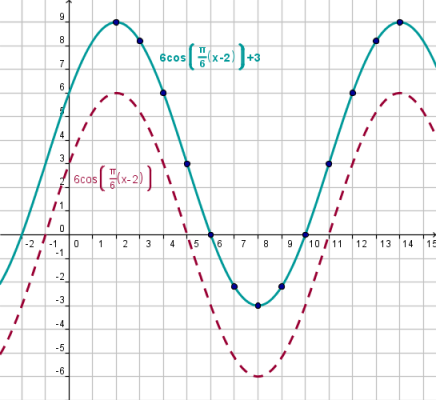Modeling with Trigonometric Functions

Objectives

Whe finishing this lesson you should be able to:

Make fundamental transformations with Trigonometric Functions.
Identify transformed trigonometric functions.
Solve application problems involving transformed trigonometric functions.

On real life problems is common to find situations that repeat themselves over and over, i.e. they exhibit a periodic behaviour. Examples of these are: daily variation of the tides and the change of temperature during a day, among others. On this lesson we will learn to model this type of situations.

Steps to Model

To model trigonometric functions we will follow the following steps:

Graph the points in order to graphically visualize the form of the corresponding curve and identify the period and the amplitude.
Map out a plan for creating the model.
Define a function base using the period and amplitude.
Transfer the function so it corresponds to the data in the problem.

Height of Tides

The following table demonstrates the variation of the water level in the bay, within a period of 24 hours. Find a model which describes the variation of the water level in function of the number of hours elapsed since 6:00 a.m.

Elapsed time (in hours)since 6:00a.m.	2	3	4	5	6	7	8	9	10	11	12	13	14
water level (in feet)	9	8.2	6	3	0	-2.2	-3	-2.2	0	3	6	8.2	9

This is a Java Applet created with GeoGebra from www.geogebra.org – Please install Java to run it.

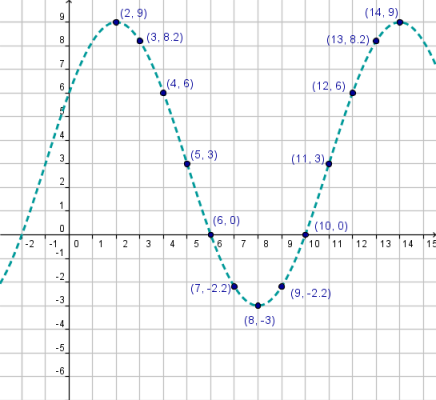
Step 1: Graph the points from the table and identify the Amplitude and the Period.

Elapsed Hours since 6:00a.m.	2	3	4	5	6	7	8	9	10	11	12	13	14
Water Level (in feet)	9	8.2	6	3	0	-2.2	-3	-2.2	0	3	6	8.2	9

sin2x

We can see that the points seem to fit a transformed cosine function.

hence, we will obtain the corresponding function if we star from:

y = cos(x)

Note: Is also valid to use the sine function but the shape formed by the points make us decide to use the cosine function.

Amplitude

From the graph we can see that the maximum value is 9 and the minimum value is -3. Hence:

amplitude = \frac{1}{2} (9 - (- 3)) = 6

Period

From the graph we see that the cosine function completes a cycle on the interval [2,9]. Hence:

period = 14 - 2 = 12

Step 2. Define the steps to follow to build the model.

On the first step we say that we decided to use the cosine function, since it fits better to the actual data.
y = cos(x)
Change the period of the function y = cos(x) ⇒ y = cos(x) to 12, as identified on step 1.
Change the amplitude of the function y = cos(kx) y = 6 cos(kx) to 6, as identified on step 1.
If necessary make an horizontal and/or vertical shift, such that the graph of the model fits the data.

Step 3. Include the period on the base function.

On step 2 we determined that the period of the function is 12.

In the lesson, Period Change of Trigonometric Functions, we learn that if x is changed to kx, the period changes. $\begin{matrix} 0 < k x < 2π \\ \frac{0}{k} < \frac{k x}{k} < \frac{2π}{k} \\ 0 < x < \frac{2π}{k} \end{matrix}$

Knowing the period, we can find the value of k, since as we know:

\frac{2 π}{k} = period

Hence:

\frac{2 π}{k} = 12

From where:

k = \frac{2 π}{12} = \frac{π}{6}

\cos (x) \Rightarrow \cos (\frac{π}{6} x)

Ex1 Graf 1

Step 4. Include the amplitude in the base function.

On step 2 we determined the amplitude as 6. Then the function must have an amplitude equal to six.

$\cos (\frac{π}{6} x) \Rightarrow 6 \cos (\frac{π}{6} x)$

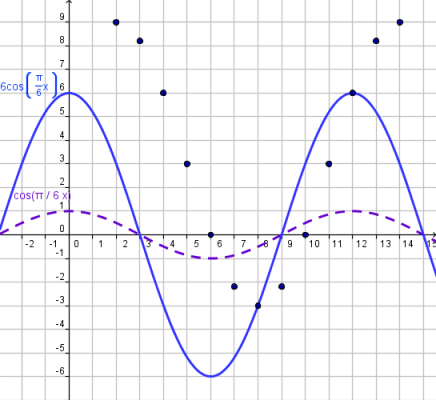
Ex1 Graf 1

Conclusion: Now we have a model that fits the period and amplitude of our data. Now, we only need to shift the graph to match the data with the graph.

Step 5. Vertical and Horizontal Shifts.

We can see that the graph is shifted two units to the right. This means we must subtract 2 to the input.

6 \cos (\frac{π}{6} x) \Rightarrow 6 \cos (\frac{π}{6} (x - 2))

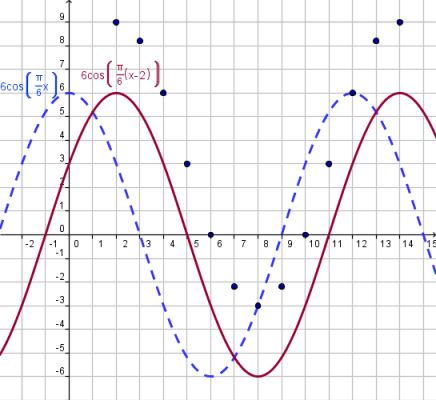Ex1 Graf 1

We can see that the graph is shifted two units up. This means we must add 3 to the output.

6 \cos (\frac{π}{6} (x - 2)) \Rightarrow 6 \cos (\frac{π}{6} (x - 2)) + 3

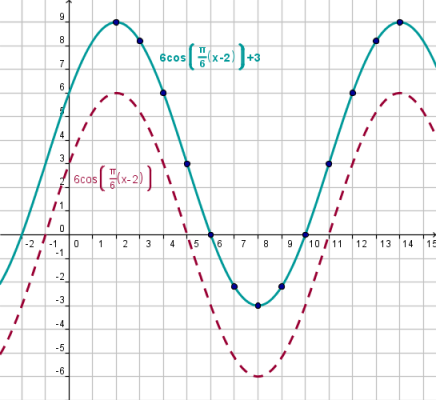Ex1 Graf 1

Step 1: Graph the points from the table and identify the Amplitude and the Period.

Month	4	5	6	7	8	9	10	11	12	13	14	15	16
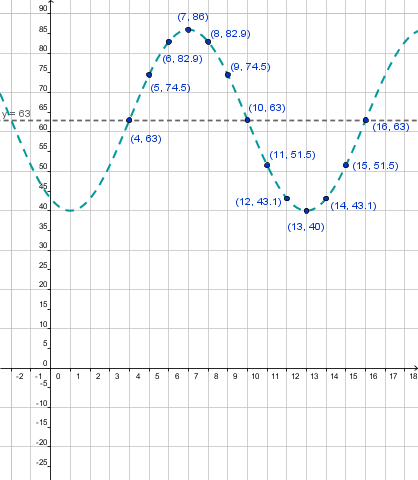
Average Temperature	63	74.5	82.9	86	82.9	74.5	63	51.5	43.1	40	43.1	51.5	63

sin2x

We can see that the points seem to fit a transformed sine function.

hence, we will obtain the corresponding function if we star from::

y = sin(x)

Note: Is also valid to use the cosine function but the shape formed by the points make us decide to use the sine function.

Amplitude

From the graph we can see that the maximum and minimum values are 86 and respectively. Hence:

amplitude = \frac{1}{2} (86 - 40) = 23

Period

From the graph we see that the cosine function completes a cycle on the interval [4,16]. Hence:

Period = 16 - 4 = 12

Step 2: Define the steps to build the model.

On the first step we say that we decided to use the sine function, since it fits better to the actual data.
y = sine(x)
Change the period of the function y = sine(x) ⇒ y = sin(x) to 12, as identified on step 1.
Change the amplitude of the function y = sine(kx) y = 23 sine(kx) to 23, as identified on step 1.
If necessary make an horizontal and/or vertical shift, such that the graph of the model fits the data.

Step 3: Include the Period on the base function.

On step 2 we determined that the period of the function is 12.

Knowing the period, we can find the value of k since we know

\frac{2 π}{k} = Period

Hence:

\frac{2 π}{k} = 12

Where:

k = \frac{2 π}{12} = \frac{π}{6}

\sin (x) \Rightarrow \sin (\frac{π}{6} x)

Ex1 Graf 1

With respect to the data the graph looks like:

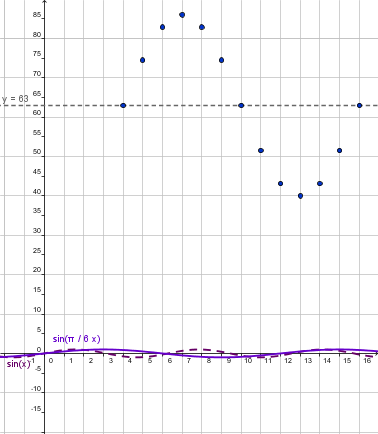
Ex1 Graf 1

Step 4. Include the Amplitude in the base function.

On Step 2 the amplitude to be equal to 23. Then the base function must have amplitude 23.

$\sin (\frac{π}{6} x) \Rightarrow 23 \sin (\frac{π}{6} x)$

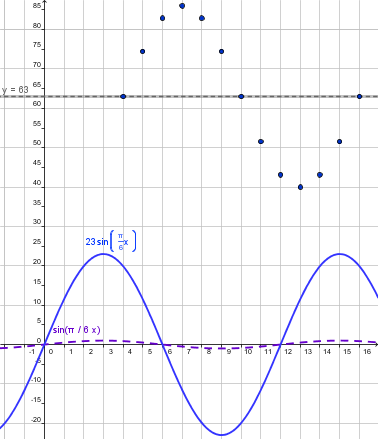
Ex1 Graf 1

Conclusion: Now we have a model that fits the period and amplitude of our data. Now, we only need to shift the graph to match the data with the graph.

Step 5. Vertical and Horizontal Shifts.

We see the graph shifted 4 units to the right. In other word we must subtract 4 to the input.

23 \sin (\frac{π}{6} x) \Rightarrow 23 \sin (\frac{π}{6} (x - 4))

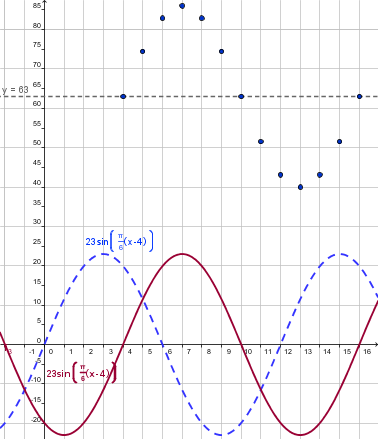Ex1 Graf 1

We see the graph shifted 63 units up. So we must add 63 to the output.

23 \sin (\frac{π}{6} (x - 4)) \Rightarrow 23 \sin (\frac{π}{6} (x - 4)) + 63

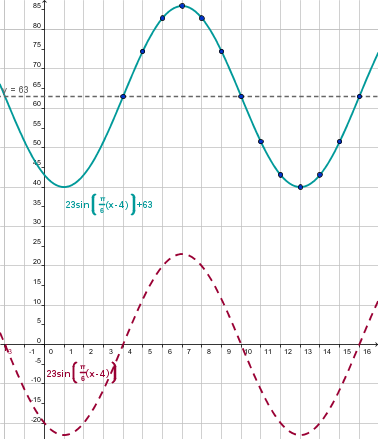Ex1 Graf 1

Step 1: Graph the points from the table and identify the Amplitude and the Period.

Year	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17
Owls Population	50	61.5	71.2	77.7	80	77.7	71.2	61.5	50	38.5	28.8	22.3	20	22.3	28.8	38.5	50

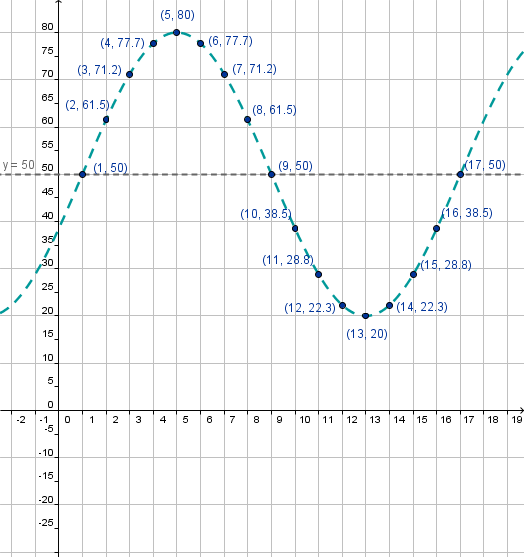
sin2x

We can see that the points seem to fit a transformed sine function.

hence, we will obtain the corresponding function if we star from::

y = sin(x)

Note: Is also valid to use the cosine function but the shape formed by the points make us decide to use the sine function.

Amplitude

From the graph we can see that the maximum and minimum values are 80 and 20 respectively. Hence:

amplitude = \frac{1}{2} (80 - 20) = 30

Period

From the graph we see that the cosine function completes a cycle on the interval [1,17]. Hence:

Period = 17 - 1 = 16

Step 2: Define the steps to build the model.

On the first step we say that we decided to use the sine function, since it fits better to the actual data.
y = sine(x)
Change the period of the function y = sine(x) ⇒ y = sin(x) to 16, as identified on step 1.
Change the amplitude of the function y = sine(kx) y = 30 sine(kx) to 30, as identified on step 1.
If necessary make an horizontal and/or vertical shift, such that the graph of the model fits the data.

Step 3: Include the Period on the base function.

On step 2 we determined that the period of the function is 16.

Knowing the period, we can find the value of k since we know

\frac{2 π}{k} = Period

Hence:

\frac{2 π}{k} = 16

Where:

k = \frac{2 π}{16} = \frac{π}{8}

\sin (x) \Rightarrow \sin (\frac{π}{8} x)

Ex1 Graf 1

With respect to the data the graph looks like:

Ex1 Graf 1

Step 4. Include the Amplitude in the base function.

On Step 2 the amplitude to be 30. Hence the base function must have amplitude equal to 30.

$\sin (\frac{π}{6} x) \Rightarrow 30 \sin (\frac{π}{8} x)$

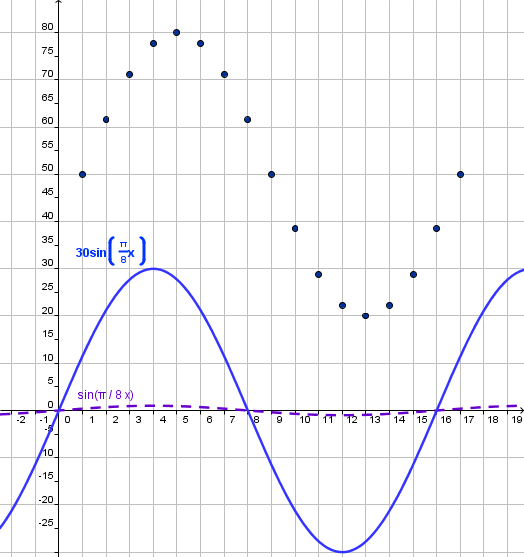
Ex1 Graf 1

Conclusion: Now we have a model that fits the period and amplitude of our data. Now, we only need to shift the graph to match the data with the graph.

Step 5. Vertical and Horizontal Shifts.

We see the graph shifted one unit to the right. In other words we must subtract 1 to the input.

30 \sin (\frac{π}{8} x) \Rightarrow 30 \sin (\frac{π}{8} (x - 1))

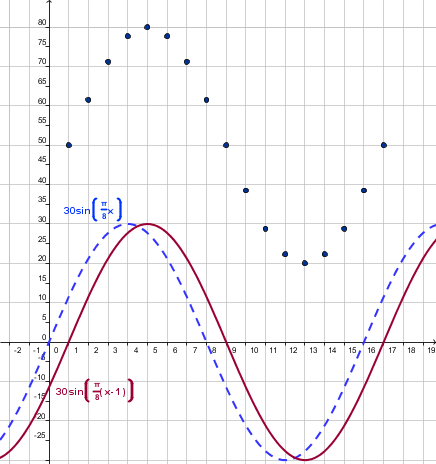Ex1 Graf 1

We see the graph shifted 50 units up. In other word we must add 50 to the output.

30 \sin (\frac{π}{8} (x - 1)) \Rightarrow 30 \sin (\frac{π}{8} (x - 1)) + 50

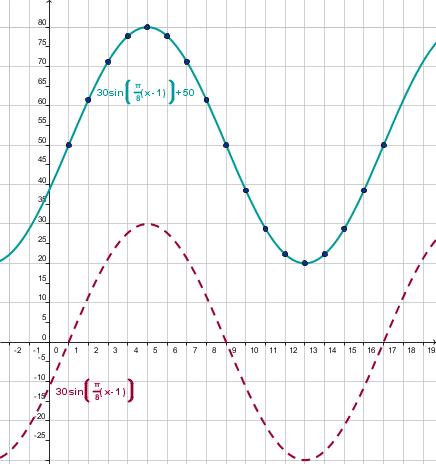Ex1 Graf 1

Step 1: Graph the points from the table and identify the Amplitude and the Period.

Seconds	1	2	3	4	5	6	7	8	9	10	11	12	13	14
Particle Height	7	8	7	3	-1	-2	-1	3	7	8	7	3	-1	-2

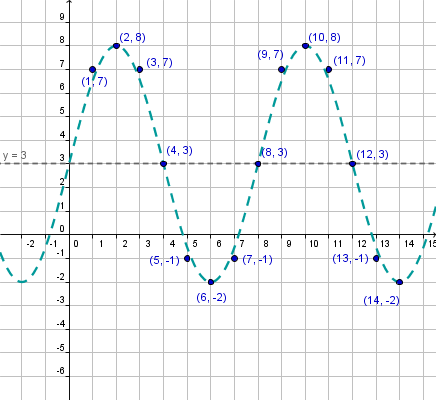
sin2x

We can see that the points seem to fit a transformed cosine function.

hence, we will obtain the corresponding function if we star from:

y = cos(x)

Note: Is also valid to use the sine function but the shape formed by the points make us decide to use the cosine function.

Amplitude

From the graph we can see that the maximum and minimum values are 8 and -2 respectively. Hence:

amplitude = \frac{1}{2} (8 - (- 2)) = 5

Period

From the graph we see that the cosine function completes a cycle on the interval [2,10]. Hence:

Period = 10 - 2 = 8

Step 2: Define the steps to build the model.

On the first step we say that we decided to use the cosine function, since it fits better to the actual data.
y = cos(x)
Change the period of the function y = cos(x) ⇒ y = cos(x) to 8, as identified on step 1.
Change the amplitude of the function y = cos(kx) y = 5 cos(kx) to 5, as identified on step 1.
If necessary make an horizontal and/or vertical shift, such that the graph of the model fits the data.

Step 3: Include the Period on the base function.

On step 2 we determined that the period of the function is 5.

Knowing the period, we can find the value of k since we know

\frac{2 π}{k} = Period

Hence:

\frac{2 π}{k} = 8

Where:

k = \frac{2 π}{8} = \frac{π}{4}

\cos (x) \Rightarrow \cos (\frac{π}{4} x)

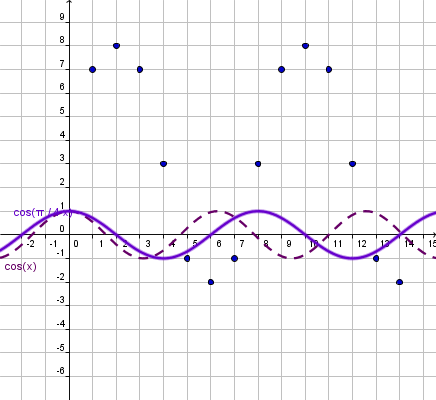Ex1 Graf 1

Step 4. Include the Amplitude in the base function.

On step 2 we determined the amplitude as 5. Then the function must have an amplitude equal to 5.

$\cos (\frac{π}{4} x) \Rightarrow 5 \cos (\frac{π}{4} x)$

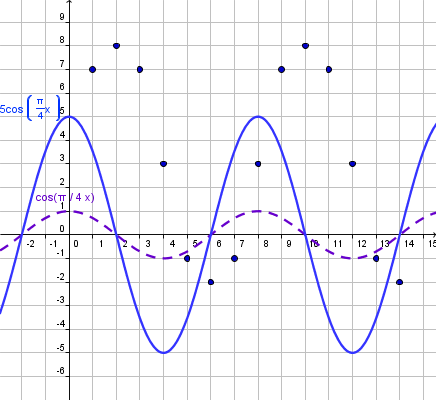
Ex1 Graf 1

Conclusion: Now we have a model that fits the period and amplitude of our data. Now, we only need to shift the graph to match the data with the graph.

Step 5. Vertical and Horizontal Shifts.

We see that the graph is shifted 2 units to the right. In other words we must subtract 2 from the input.

5 \cos (\frac{π}{4} x) \Rightarrow 5 \cos (\frac{π}{4} (x - 2))

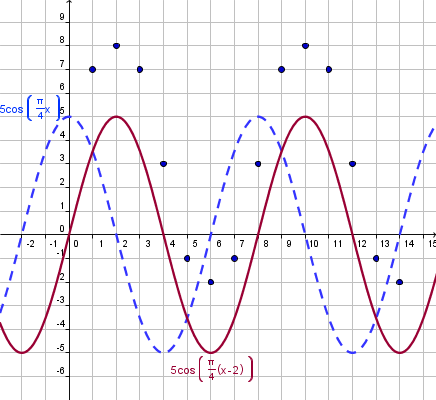Ex1 Graf 1

We see that the graph is shifted 2 units up. In other words we must add 2 to the output.

5 \cos (\frac{π}{4} (x - 2)) \Rightarrow 5 \cos (\frac{π}{4} (x - 2)) + 3

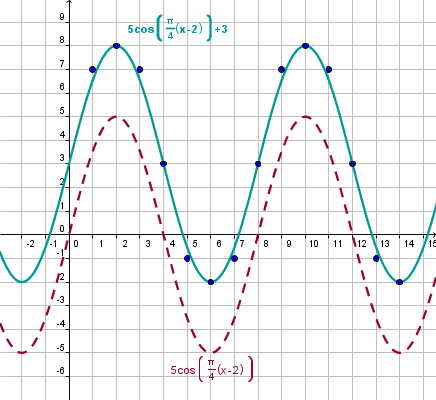Ex1 Graf 1


Click the buttons to see the steps of the model

Temperature Change

A research was conducted on the temperature of a city, measures of the average temperature were made from April 2010 to April 2012. The data is registered in the following table:

Mes	4	5	6	7	8	9	10	11	12	13	14	15	16
Average Temperature	63	74.5	82.9	86	82.9	74.5	63	51.5	43.1	40	43.1	51.5	63


Click the buttons to see the steps of the model

Predators Population

A research was conducted on a forest populated by owls whose main food resource are mice. The average population of owls for was registered for 13 years as is shown in the following table:

Year	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17
Owls Population	50	61.5	71.2	77.7	80	77.7	71.2	61.5	50	38.5	28.8	22.3	20	22.3	28.8	38.5	50


Click the buttons to see the steps of the model

Oscillation

The following table shows the height of a particle hanging from a spring on a roof per second after the initial movement:

Seconds	1	2	3	4	5	6	7	8	9	10	11	12	13	14
Particle Height	7	8	7	3	-1	-2	-1	3	7	8	7	3	-1	-2


Click the buttons to see the steps of the model

Summary

Now that you have completed the tutorial you must be able to:

Make fundamental transformations with Trigonometric Functions.
Identify transformed trigonometric functions.
Solve application problems involving transformed trigonometric functions.